This page is available as a Word document.

A shocking number of patients die every year in United States hospitals as the result of medication errors, and many more are harmed. One widely cited estimate (Institute of Medicine, 2000) places the toll at 44,000 to 98,000 deaths, making death by medication "misadventure" greater than all highway accidents, breast cancer, or AIDS. If this estimate is in the ballpark, then nurses (and patients) beware: Medication errors are the forth to sixth leading cause of death in America.

How many medication errors are miscalculation errors? No one really knows since by some estimates as little as one in ten errors are reported (Pepper, 2002). Of reported errors one FDA study (Thomas, Hoquist, Phillips, 2001) found that 7% were due to "miscalculation of dosage or infusion rate." Combining this estimate with the estimate for total deaths, as many as 3,000 to 6,800 deaths are caused annually by medication math errors. This would mean that in the average hospital one patient dies every year or two because someone makes a miscalculation, and one or two patients are sub-lethally harmed each month. As future nurses, then, there is a distinct possibility that we will harm, or even cause the death of, a patient over the course of our career.

If we believe the adage "first do no harm" applies to us, then what can we possibly do to minimize miscalculation errors? If we only aim to pass Medication Math with an 80% or above, are we setting the bar high enough? It might be late some Saturday night, you're the only RN on the floor, the hospital pharmacy is closed, and it's up to you to calculate a needed dosage. Surely getting the right answer only 80% of the time is not acceptable. Perhaps the problem you need to solve is a little different than any you've seen before or recall seeing in the textbook. How confident will you be that your calculation is correct?

The time to build confidence is while we are students. I suggest that as conscientious students we should aim for 95% or better. We should, then, carefully study, learn from, and thereby avoid repeating what mistakes we do make, so that by the time we are working in the real world we can be confident that, if we are vigilant enough, we can approach 100% proficiency. Since "to err is human," we will always be at risk of not achieving a goal of 100% proficiency, but we cannot aim for less, and knowing that we are always at risk will make us extremely careful.

Neither effort, desire to avoid error, nor carefulness, however, is enough. We need the right tools and techniques that will help us avoid miscalculations. I believe that dimensional analysis is the most appropriate tool available to us. It is, by far, the best method of solving medication math problems with the least chance of making errors. As nurses we're not likely to ever use whatever algebra, trigonometry, calculus, or statistics we may know and (even better?) we need make no effort to learn these subjects, but we should strive for a deep understanding of, and proficiency in, dimensional analysis (DA).

The good news is that mastery of DA is not at all an unobtainable goal. While few could master a vast subject such as algebra in a lifetime, most students should be able to master DA in a few weeks of focused effort. Mastery would mean the ability to solve any problem that could crop up, no matter how it is presented, while avoiding pitfalls. Needless to say, if I thought that nursing students were mastering DA, I wouldn't be writing this paper.

The bad news, then, is that most nursing students have a weak understanding of DA. Most can follow examples given in the textbook; they can then solve all the practice problems that follow the same general format. If quizzes or tests also follow the textbook examples, most students succeed brilliantly.

That all is not well, however, is apparent went problems do not meet expectations. One sophomore class stumbled badly on a test apparently for this reason. They could all follow, if imitatively, the examples in the textbook, and could therefore do all the practice problems, but when the test presented problems in an unexpected format, most failed--only 2 students passed the test. In their final semester before graduating as RNs, a third failed another test. This suggests a weak understanding of DA.

Unfortunately most students have almost, but not quite, a complete understanding of DA. I believe this is due to the textbook used (Clinical Calculations: A unified approach, 4th ed.) almost, but not quite, presenting a complete description of DA. It may be that there are too few nurse/mathematicians to write textbooks, and so a weak foundation for DA is laid for students to build on. My aim in writing this paper is to provide nursing students with a more robust foundation to build on, and perhaps reduce future misadventures. I am not a mathematician, but I have been doing DA for 30 years, have made refinements in the technique over that time, and as a substitute teacher I have taught it to middle and high school students.

Dimensional analysis is your friend. Embrace it; learn to love it. It is our best defense against doing harm to a patient by miscalculation.

The following summary can be used as a guide for doing DA. Some familiarity with DA is assumed. See Appendix A for an introduction to DA. The examples cited below refer to examples used in Appendix A. While not all steps listed below will be needed to solve all problems, I have found that any problem that can be solved using DA will yield its answer if the following steps are followed. I would not suggest memorizing the sequence of steps, but rather understanding and practicing them. Understanding is more durable than memory.

a. Rephrase if necessary using "per." Example: You want to know "milligrams per liter."

1. What are you given by the problem, if anything? Example: "In one minute, you counted 45 drops."
• Rephrase if necessary. Think: "Drip rate is 45 drops per minute."
• Translate into math terms using abbreviations, e.g. "45 gtt/min"
• If a given is in the form mg/kg/day, rewrite as mg/kg x day (see example 4)
• If a percentage is given, e.g. 25%, rewrite as 25/100 with appropriate labels (see example 5)
2. Determine conversion factors that may be needed and write them in a form you can use, such as "60 min/1 hour." You will need enough to form a "bridge" to your answer unit(s). See example 1.
• Factors known from memory: You may know that 1 kg = 2.2 lb, so write down "1 kg/2.2 lb" and/or "2.2 lb/1 kg" as conversion factors you may need.
• Factors from a conversion table: If the table says "to convert from lb to kg multiply by 2.2," then write down "2.2 lb/1 kg"
3. Setup the problem using only what you need to know.
1. Pick a starting factor.
• If possible, pick from what you know a factor having one of the units that's also in your answer unit and that's in the right place. See example 1.
• Or pick a factor that is given, such as what the physician ordered.
• Note that the starting factor will always have at least one unit not in the desired answer unit(s) that will need to be changed by cancelling it out.
2. Pick from what you know a conversion factor that cancels out a unit in the starting factor that you don't want. See example 1.
3. Keep picking from what you know factors that cancel out units you don't want until you end up with only the units (answer units) you do want.
4. If you can't get to what you want, try picking a different starting factor, or checking for a needed conversion factor.
5. If an intermediate result must be rounded to a whole number, such as drops/dose which can only be administered in whole drops, setup as a separate sub-problem, solve, then use the rounded off answer as a new starting factor. See example 9.
4. Solve: Make sure all the units other than the answer units cancel out, then do the math.
1. Simplify the numbers by cancellation. If the same number is on the top and bottom, cancel them out.
2. Multiply all the top numbers together, then divide into that number all the bottom numbers.
3. Double check to make sure you didn't press a wrong calculator key by dividing the first top number by the first bottom number, alternating until finished, then comparing the answer to the first one. Miskeying is a significant source of error, so always double check.
4. Round off the calculated answer.
• Be realistic. If you round off 74.733333 to 74.73 mL that implies that all measurements were of an extreme accuracy and that the answer is known to fall between 74.725 and 74.735, or 74.73 + 0.005 mL. A more realistic answer would probably be 74.7 mL or 75 mL. See example 6.
• If you round to a whole number that implies a greater accuracy than is appropriate, write your answer to indicate a range, such as 75 + 5 mL. See example 9.
5. Add labels (the answer unit) to the appropriately rounded number to get your answer. Compare units in answer to answer units recorded from first step.
5. Take a few seconds and ask yourself if the answer you came up with makes sense. If it doesn't, start over.

This is a fairly bare outline, so refer to Appendix A for examples. The steps are best taught, rather than read, and so would serve better as a guide to tutoring students than as a self-teaching guide.

Anything we can do to reduce errors by even the smallest degree is worth doing. How we choose to write down a DA problem, for example, can make a difference. Should we just keep the answer unit in mind, circle it in the problem, or actually write it down? At best we will hit what we aim for, so we must be very clear about what we want, about the answer unit(s) we are aiming for. Reading the problem with the sole, focused purpose of determining the answer unit, then writing it down (least we forget or get confused later on) is an example of good technique.

You can be sloppy and still get the right answer most of the time, but eventually you'll blunder because of poor technique. You'll triumphantly, like me, write down "4.3 mL/min" as your answer forgetting that you were supposed to calculate "mL/hr" and all because you neglected to write down the answer units and compare them with your answer.

DA problems are often written in fraction form, even though they are factors and shouldn't be confused with fractions:

When it comes time to do the math, the first number is can be overlooked, especially if you're using scratch paper with other problems on it, perhaps because it is visually different and not in line with other values. An error of omission is less likely using the following non-fraction format:

This format is more visually integrated, more bridge like, and is more appropriate for working with factors. It is also less confusing when doing amounts-per-body-weight-per-dose or day calculations (see Example 4 in Appendix A).

Occasionally a factor like "50 kg" will need to be divided rather than multiplied which could cause confusion or errors when doing the math if the division sign is not noticed when written in fraction form.

Since the first factor is normally multiplied, students might stumble if division is required. When written in factor form using bars, mistakes and confusion is minimized:

This is, then, another reason to avoid the fraction format.

Perhaps with the exception of conversion factors you have memorized, it is advisable to actually write down, in "math terms" or factor form anything given to you by the problem as well as any conversion factors you had to look up. Often the hardest part of a problem is translating fuzzy English phrasing into crisp math terms you can use.

Use abbreviations that are clear and label numbers fully. Using a degree symbol for hour instead of "hr" is an invitation to error. If the degree symbol is written a little too big it could be mistaken for a zero resulting in an order of magnitude error. When doing the math, the brain is looking for numbers and could see "10" where a "1" is meant:

Another abbreviation to avoid is using mu (m) for micro as in microgram (mg). When handwritten, "m" can look like an "m" and so "mg" looks like "mg" which could lead to a three orders of magnitude error. The preferred abbreviation, then, is "mc" for "micro" as in "mcg" for "microgram."

If you were doing calculations involving milliliter volumes of three solutions, A, B, and C, then do not use "mL" alone without specifying "mL of what?" Your labels, then, would be in the form "23 mL A" or "3 mL C" and you would know to only cancel out "mL B" with "mL B." Whenever you label any number with a unit of measure, always be aware that you are dealing with grams of something or liters of something, and so on. It may therefore be helpful to label fully rather than minimally. Writing "25 mL NS" is much clearer than just "25 mL." In some problems, failure to fully label numbers can lead to serious confusion and error.

Errors may be unavoidable in absolute terms, but we can minimize the number of errors we make. A good understanding of dimensional analysis is our best bet to avoid miscalculation errors. With practice all nursing students can acquire a high level of proficiency in doing medication math.

R. Eric Lee

busybee@theriver.com

Institute of Medicine (2000) To Err Is Human: Building a Safer Health System National Academy Press. Available online: http://www4.nas.edu/news.nsf/isbn/0309068371?OpenDocument

Pepper, Ginette A. (2002) Errors in drug administration by nurses from Understanding and Preventing Drug Misadventures Conference. Available online: http://www.ashp.org/public/proad/mederror/pep.html

Thomas MR; Hoquist C; Phillips J. (Oct. 1, 2001) Med error reports to FDA show a mixed bag. Drug Topics; 145(19); 23. Available online: http://www.fda.gov/cder/drug/MedErrors/mixed.pdf

Dimensional analysis (also known as the factor-label method or unit-factor method) is by far the most useful math trick you'll ever learn. Maybe you've learned some algebra, but do you ever use it? Ever foresee using it? For most people the answer is "not after the final exam."

For a fraction of the effort needed to learn algebra, you too can learn "dimensional analysis." First off, however, let's get rid of the big words. What this is all about is just conversion--converting one thing to another. This is something you will have occasion to do in real life. This is seriously useful stuff.

This trick is about applied math, not about numbers in the abstract. We're talking about measurable stuff you can count or measure. Anything you measure will have a number with some sort of "unit of measure" attached. A unit could be miles, gallons, miles per second, peas per pod, or pizza slices per person.

First, don't panic. If you have no idea what the answer is or how to come up with an answer, that's fine--you're not supposed to know. You're not going to solve THE problem. What you are going to do is break the problem down into several small problems that you can solve.

Here's your first problem:

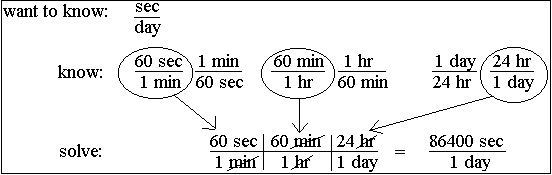
1. Ask yourself, "What units of measure do I want to know or have in the answer?" In this problem you want to know "seconds in a day." After you figure out what units you want to know, translate the English into Math. Math is a sort of shorthand language for writing about numbers of things. If you can rephrase what you want to know using the word "per," which means "divided by," then that's a step in the right direction, so rephrase "seconds in a day" to "seconds per day." In math terms, what you want to know is:

2. Ask, "What do I know?" What do you know about how "seconds" or "days" relate to other units of time measure? You know that there are 60 seconds in a minute. You also know that in 1 minute there are 60 seconds. These are two ways of saying the same thing. You know that there are 24 hours in a day (and in one day there are 24 hours). If you could now connect "hours" and "minutes" together you would have a sort of bridge that would connect "seconds" to "days" (seconds to minutes to hours to days). The connection you need, of course, is that there are 60 minutes in an hour (and in one hour there are 60 minutes). When you have this kind of connection between units, then you know enough to solve the problem--but first translate what you know into math terms that you can use when solving the problem. If in doubt, write it out:

All of these statements, or conversion factors, are true or equivalent (60 seconds = 1 minute). All you need to do now is pick from these statements the ones that you actually need for this problem, so....

3. Ask, "From all the factors I know, what do I need to know?"

Remember that you want to know:

So pick from the things you know a factor that has seconds on top or day(s) on the bottom. You could pick either of the following two factors as your "starting factor:"

Write down your starting factor (say you pick 60 seconds per 1 minute):

Now the trick is to pick from the other things you know another factor that will cancel out the unit you don't want. You start with "seconds" on top. You want "seconds" on top in your answer, so forget about the seconds--they're okay. The problem is you have "minutes" on the bottom but you want "days." You need to get rid of the minutes. You cancel minutes out by picking a factor that has minutes on top. With minutes on top and bottom, the minutes will cancel out. So you need to pick 60 minutes per 1 hour as the next factor because it has minutes on top:

You now have seconds per hour, since the minutes have cancelled out, but you want seconds per day, so you need to pick a factor that cancels out hours:

4. Solve it. When you have cancelled out the units you don't want and are left only with the units you do want, then you know it's time to multiply all the top numbers together, and divide by all the bottom numbers.

In this case you just need to multiple 60x60x24 to get the answer: There are 86,400 seconds in a day.

Here's how this problem might look if it were written on a chalkboard:

Remember that you don't need to worry about the actual numbers until the very end. Just focus on the units. Plug in conversion factors that cancel out the units you don't want until you end up with the units you do want. Only then do you need to worry about doing the arithmetic. If you set up the bridge so the units work out, then, unless you push the wrong button on your calculator, you WILL get the right answer every time.

Let's go through the steps:

• Don't panic
• What do you want to know? This one's easy: hours in a year, or better, hours per year
• Translate into math terms:

• What do you know that you might need to use? You know that there are 24 hours in a day, 7 days in a week, 4 weeks in a month, 12 months in a year, and about 365 days in a year. The converse, of course, is also true: In one day there are 24 hours, in one week there are 7 days, in one month there are 4 weeks, in one year there are 12 months, and in one year there is about 365 days (actually closer to 365.25 days).
• Translate into math terms--writing them all down can't hurt:

• Pick a starting factor. Since you want hours on top (or years on the bottom), you could start with 24 hours per day:

• Now pick whatever factors you need to cancel out day(s):

• Keep picking factors that cancel out what you don't want until you end up with the units you do want:

• Do the math. You have all the units cancelled out except hours per year, which is what you want, so when you do the math, you know you'll get the right answer:

• But wait, why not go from "hours" to "year" using the fact that there are 365 days per year?

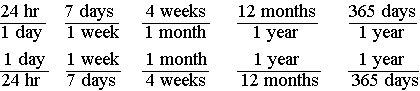
Oh no! There is a 696-hour difference between the two answers! How can this be? Exact answers can only be obtained if you use conversion factors that are exactly correct. In this case there are actually more than 4 weeks in a month (about 4.35 weeks per month). Since there is a bit more than 365 days in a year, a more accurate answer still, to the nearest hour, would be that there are 8766 hours in a year. The point of this example is that your answer can only be as accurate as the conversion factors you use.

Sometimes both the top and bottom units need to be converted:

If you were to do this one on the blackboard, it might look something like this:

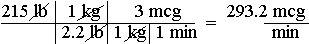
You want your answer to be in feet per second. You are given 50 miles per hour. Normally you can use any value given by the problem as your starting factor. One thing you know, then, is given. The other things you just know or have to look up in a conversion table. Although every conversion factor can be written two ways, you only wrote each one way. That's because you know you can always just flip it over and then use it. To solve this problem you had to flip the 60 min/hour and 60 sec/min factors over. With practice you won't even need to write down what you know, you'll just write down the last part, do the math, and get the right answer.

 Example 4

You have come down with a bad case of the geebies, but fortunately your grandmother knows how to cure the geebies. She sends you an eyedropper bottle labeled:

• This problem is a bit more challenging, but don't panic. Break the problem down into a bunch of small problems, and tackle each one by one.
• What do you want to know? In order to take one dose 4 times a day you need to know how many drops to take per dose.
• Translated into math terms you want the answer to be in:

• What do you know? Well, you know you weigh 160 pounds. You know that you need to take 4 doses per day (implied). You know that you need to take 1 drop per 10-lbs. body weight per day.
• Translate this into math terms:

• The problem now is the last factor. What can you do with such an odd factor? You rewrite it so it is in a different form that you can use. What you do is multiply the middle term by the bottom term:

• So whenever you have a triple-decker, use this trick to rewrite the factor.
• Now you should be able to solve the problem. The one thing you know that isn't a conversion factor is that you weigh 160 lbs., so use that as your starting factor:

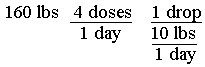
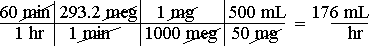
If you had wanted to know how many drops per day to take, you would have just left off the last conversion factor, which would give you an answer of 16 drops/day.

You're not told what answer unit to use, but ounces would work since there are 32 oz in a quart. If the only thing you had to measure bleach with was in millimeters, then you would pick "mL" as your answer unit.

When you are given something like "5 percent" or "5%" by a problem, you need to translate it into math terms you can use. "5%" means 5 per 100 or 5/100, but 5 what? per 100 what? You need to label the numbers appropriately. In this example you write down "5 oz bleach/100 oz bleach solution" or just "5 oz B/100 oz BS" as a factor you are given. If you were going for milliliters, then you would use "5 mL B/100 mL BS." The top and bottom units must be the same or equivalent, but otherwise can be any units you may need. If you had 5 gal. bleach/100 gal. bleach solution, then you would still have a 5% bleach solution.

Setting up and solving this problem is now easy:

So you would add 1.6 oz bleach to a quart measuring cup, then add water (30.4 oz) to make 32 ounces of 5% bleach solution.

Example 6

Unless the next stop is Las Vegas and you're feeling really lucky, you should turn around and get some more gas. Your calculator reads "74.4" exactly, but if you believe what it says, then you believe that when the car runs out of gas, it will have gone some where between 74.35 miles and 74.45 miles or 74.4 + 0.05 miles. Obviously the "point four" is meaningless, so you round to 74. Is 74 the right answer? If you think it is, then you think your car will go some where between 73.5 miles and 74.5 miles before running out of gas. When you run out of gas, what chance do you think you'll have of having gone 74 + 0.5 miles? A proverbial "fat chance" would be a good guess.

When you're given something like a "quarter tank" you should wonder just how accurate such a measurement is. Can you really divide 18.6 by 4 and conclude that there really is 4.65 gallons of gas in the tank? The last time you figured mileage you came up with 16 miles/gallon, but is the engine still operating as efficiently? Are the tires still properly inflated? Will the next 73 miles be uphill? Do you have a head wind? Surely a calculated estimate of 74 miles is overly precise. A realistic answer, then, might be 74 + 10 miles. You realize you could run out of gas anywhere between 66 and 84 miles, so you finally and correctly conclude that you have a slightly less than a 50/50 chance of running out of gas before reaching the next gas station.

The point of this example is to remind you that dimensional analysis is applied math, not abstract math. The numbers used should describe the real world in so far as possible and indicate no more accuracy than is appropriate. If you overlook this point, you might have a five-mile walk to the next gas station.

1. Ask yourself, "What do I want to know?" In this case, how much money is the pizza going to cost you, which in math terms is: cost (in dollars) per party, or just $/party. This is your "answer unit." This is what you are looking for.

2. Ask, "What do I know?" Write it all down, everything you know: one pizza will cost you $14.78 (in math terms 1 pizza/$14.78). You also know that for $14.78 you can buy one pizza ($14.78/1 pizza). It can be important to realize that every conversion factor you know can be written two ways. One of these ways may be needed to solve the problem and the other won't, but in the beginning you don't know which, so just write them both ways. Continue writing down other things you know. You know, or hope, that only 15 people will be eating pizza (15 persons/1 party), or for this one party, 15 people will come (1 party/15 persons). You also know there will be 12 slices per pizza (12 slices/1 pizza), or that each pizza has 12 slices (1 pizza/12 slices). The last thing you know is that each person gets 4 slices (1 person/4 slices), or that you are buying 4 slices per person (4 slices/person). Math is a language that is much briefer and clearer than English, so writing every thing you know in math terms, here's what you might have written down:

3. Ask, "From all the things above I know, what do I actually need to know to figure out the problem?"

Remember that you want to know $/party, so pick one of the things you know that has either dollars on top, or "party" on the bottom. Let's start with $14.78/pizza as the starting factor. Great, you got dollars on top, but "pizza" on the bottom where you want "party." To get rid of "pizza" pick one of the things you know that has "pizza" on the top. "Pizza" over "pizza" cancels out, so you get rid of the "pizza:"

Okay, you now have dollars per slice, but you want dollars per party, so now what? Easy, just keep picking from the things you know whatever cancels out the units you don't want. The numbers go with the units, but don't worry about numbers, just pay attention to the units. So you pick 4 slices/1 person to get rid of "slices," then 15 persons/1 party to get rid of "person(s):"

Now multiply all the top numbers, and then divide by any bottom numbers to get the right number. Finally add the units that are left over to the number to get the answer you wanted. Using this method, you can hardly go wrong unless you push the wrong button on your calculator.

By the way, how many pizzas should you order? Figuring this out should be as easy as....

Okay, enough easy problems, let's try something harder. Well, not really harder, just longer. The point of this example is that no matter how ridiculously long your conversion might be, long problems are not really more difficult. If you get the point, then skip this example; otherwise read on.

1. What do you want to know? $/person round trip--the answer unit(s).

2. What do you know so far? There will be 3 persons going on a round trip (3 persons/1 round trip), or in the planned round trip 3 persons will be going (1 round trip/3 persons), it will be a 2015 km trip one-way (2015 km/one-way trip), or one-way is 2015 km (one-way trip/2015 km), there are 2 one-way trips per round trip (2 one-way/round trip), there is 11 cents per peso (11 cents/1 peso), or one peso is worth 11 cents (1 peso/11 cents). Finally you know that one liter of gas costs 5.8 pesos (1 liter/ 5.8 pesos), or 5.8 pesos will buy you 1 liter (5.8 pesos/1 liter).

You know a lot, but still not enough. Knowing the number of miles in a kilometer, or liters in a gallon would be nice, but one of your friends recalls that there is 39.37 inches in a meter and the other is sure that there is 4.9 ml in a teaspoon. This still isn't enough. You might need to know that there are 1000 meters in a kilometer, 1000 ml in a liter, 100 cents per dollar, 12 inches to the foot, and 5,280 feet to the mile, but then you already knew that.

Almost enough, but how can you get from teaspoons to gallons? Simple, call your mom. She knows that there are 3 teaspoons in a tablespoon, 16 tablespoons in a cup, 2 cups in a pint, 2 pints in a quart, and 4 quarts in a gallon. Wow, that's a lot of things to know, but it should be enough. Write it all down in math terms and see what you have:

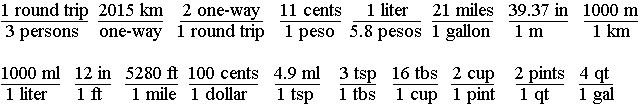
3. What do you need to know from the above? If any of the above are upside down from what you end up needing, just turn them over, then use them. This problem looks harder than it is. Since we want to end up with $/person, let's start with:

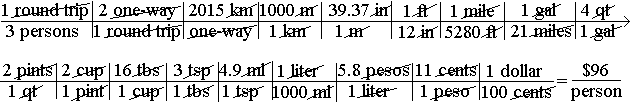
Even with 18 factors to plug in to get your answer, it's still pretty much a no-brainer whether you have two or 30 factors. If you know enough conversion factors and set the "bridge" up correctly to cancel out all unwanted units, then you get the correct answer. You may have to look up a few conversion factors you don't know, but once you do, you're home free. Looking up the number of liters per gallon or miles in a kilometer would have saved quite a few steps, but if you can remember any relationship you can still figure out your answer. It takes a little longer, but really adds nothing to the inherent difficulty. 

Now this one is a bit hard if you haven't paid close attention to the previous examples.

Try working this one out before reading further.

First, what do you want to know? You want to know how long the bottle will last. You could figure out days/bottle or weeks/bottle and see if the bottle will last longer than 3 weeks or 21 days. So you write down "AU=days/bottle"

What do you know to start off with that you might need to know? You write down the following:

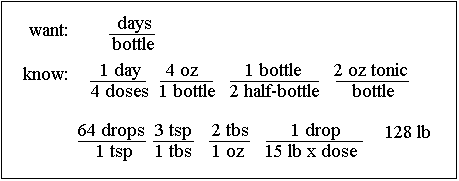
You realize that if a 4-oz bottle is half-full, then there is 2 oz of tonic in it, but you could figure it out dimensionally if you wanted to:

You would then end up with "days/half-bottle" in your answer, but it's easier to just go with 2 oz/bottle as you're given.

What should you use as a starting factor? You pick 128 lb because it's something you're given and it seems lonely. You set the problem up:

Houston, we have a problem. You ended up with units reversed from what you wanted. You figured out how much of the bottle you would use in one day. What to do? You could hit the 1/x button on your calculator if it had one, or invert the answer by dividing 1 by 0.044, or start over with 128 lb on the bottom. What? Can you do that? Sure you can. You could even put 128 lb on the end and on the bottom, or put it in the middle somewhere. You decide to start over, this time picking a starting factor that already has "day" or "bottle" in the right place.

So, it looks like you'll have enough. At some point you need to know how many drops per dose you will need to take, so you figure it out:

As a practical matter, you can't take 8.533 drops per dose; you have to round off. At this point you realize that when you calculated 22.5 days/bottle, you were not figuring on 9 drops/dose. You decide to recalculate to see if rounding up to 9 makes a significant difference.

You note a small difference, but conclude that you have just enough geebie tonic. Concluding that you have enough, however, and having enough may not be the same thing. The story continues:

You finally realize there might not have been 2.0 oz of tonic in the bottle to begin with. A measurement like "half a bottle" should not inspire great certainty. You wish you had measured the amount and found that the bottle contained 2.0 + 0.05 oz of tonic, but what you were given, more or less, was that you had 2 + 0.5 oz of tonic. There could be anything from 1.5 to 2.5 oz in the bottle. Recalculating using the low and high values, you find you had enough tonic to last somewhere between 16 and 26 days. If you had figured out the correct answer of 21 + 5 days the first time, you would have realized you had only slightly less than a 50/50 chance of running out, and would have gone to see Granny for a refill.

• Don't panic.
• Figure out what answer unit(s) you want to end up with. This is usually easy.
• Write down, in math terms, everything you know that relates to the problem. You may need to read the problem several times, rephrasing parts of it, so you can translate everything into math terms. You may need to look up a few conversion factors, but that's inconvenient, not difficult.
• Pick a starting factor. If possible pick one that already has one of the units you want in the right place. Otherwise start with something you are given that is not a conversion factor.
• Plug in conversion factors that allow you to cancel out any units you don't want until you are left with only the units you do want (your answer units).
• If you can't solve the problem, pick a different starting factor and start over.
• Do the math. You may be less apt to make an error if you first multiply all the top numbers, then divide by all the bottom numbers. Now double-check your calculations.
• Ask yourself if the answer seems right or reasonable. If not, recheck everything.

Determining the answer unit or units is crucial; they are not always obvious and can be challenging to determine. For some problems, reading the problem correctly is the only challenge. Students need to be able to translate sometimes convoluted English descriptions of a problem into clear, properly labeled factors they can later use to solve the problem. This skill is not emphasized in the textbook. If the answer unit is always given in the examples used, then this is because the examples have been contrived to be more simple and consistant than actual problems tend to be.

In some real-world problems no starting factor is given, or several possible starting factors are given with no way to decide, initially, which to use. It is preferable, in such cases, to determine everything you know that might be relevant to solving the problem, then decide, after the answer unit is determined, which of the factors you know would make an appropriate starting factor.

All examples used throughout the text use only numbers having a single unit attached for starting factors. Apparently "1 hour" is an acceptable starting unit, but "250 mL/hour" is not. This is not correct as starting factors are often in the form of "something per something." Indeed, some problems cannot be solved if they have a single unit starting factor (see example 3 in Appendix A).

While many conversion factors are approximations, and fraction of a percent errors are unimportant in medication math, 10 percent errors are a bit worrisome. Equating 1 grain with 60 milligrams when the actual equivalency is closer to 64.8 mg, is questionable, as is equating liters and quarts, or 1 mL to 15 minims (actually 1 mL = 16.23 minims). It is possible to solve a problem and come up with answers that differ by as much as 10% depending on which approximate conversion factors you decide to use. If + 5% errors are acceptable, then, as an aside, any answer to a test question that is within 5% of the correct answer should be counted as correct. It is slightly ludicrous to insist on carrying out calculations to two decimals, rounding to the nearest tenth, when far greater errors can be introduced by using loose approximations.

When, in chapter 6, a problem involving amount/body weigh/day comes up, the solution is presented in an unorthodox way. The problem (p. 49) gives 25 mg/kg/24 hr. When doing dimensional analysis it is essential that all the units given should be used and accounted for. Ignoring a given unit, then pulling it out of thin air at the end is poor technique, yet this is what the textbook does. The solution is given as:

The problem is that the correct answer units should be how many mL should be administered per day, or "mL/day." Omitting the "per day" part doesn't alter the fact that that is what you want to know--not per hour, not per dose, but per day. There is actually a simple rule that applies here. For example, when acceleration is measured in feet per second per second, it is not written as ft/sec/sec, but as ft/sec² because ft/sec/sec is equal to ft/sec x sec. So if you're given mg/kg/day, the preferred way to deal with such a "triple decker" is to rewrite it as mg/kg x day. In this form it can be used, all undesired units cancel, and you end up with the desired answer with the right units attached:

If the problem called for "mL/dose" given 4 doses per day, then the solution is straightforward:

If "day" were omitted, however, this problem would become more difficult to solve. The textbook method is to calculate "mL," then divide by 4 to get "mL/dose." Students must remember to perform this final "critically important" step which would not exist if if better technique were used. As the text acknowledges, "it is easy to forget to divide the total daily dose into the prescribed number of doses, thus greatly increasing the risk of administering an overdosage."

Problems of this sort are common, and it is unfortunate that the authors neglect to show students how to logically deal with them. The risk of confusing some students by introducing a new rule can hardly be worth the risk of error introduced by teaching a flawed technique.

In Chapter 10, page 184, an example is shown, as a model for students to follow, to determine how many mcg/min must be administered to a 215 lb patient at 3 mcg/kg/min:

In this example, at least, minutes are not omitted then added at the end, and the technique is not even erroneous, but merely confusing to many students and visually awkward. A student might try to logically extend this technique to determine mL/hr:

The student who notices that the answer doesn't make sense might wonder what went wrong. Would they realize that when "mcg" was cancelled that "3 1/min" was left requiring the use of 60 min/1 hr instead of 1 hr/60 min? Trying to explain how to work around the poor technique employed by this example only digs a deeper hole. The better response to student confusion would be to have them but a big X mark over this section of the textbook and show them a sensible way to set it up:

Another case of flawed technique arises in Chapter 10. Students are given problems that require converting from mL/hr to gtt/min, and are shown conversion equations like the following:

The problem, again, is that the correct answer unit is "gtt/min" and not "gtt" as it appears. The correct answer is just pulled out of nowhere and declared to be "33 gtt/min." The initial starting factor of "1 min" is spurious. It is not a given, and it means absolutely nothing to say that you know "1 min" or "1 hour" or "1 hotdog." If such meaningless starting factors are simply omitted from such examples, the problems are perfectly setup to yield the correct answers with the correct answer units. It seems that the pseudo-starting factor is used to avoid having a starting factor with more than one unit attached. As mentioned, however, there is no such requirement when doing dimension analysis. In the above example "90 mL/1 hr" would make a logical and perfectly good starting factor.

Students should be told to just ignore the nonsensical "1 min" and "1 hour" starting factors. If you were to introduce "1 hour" as a starting factor in example 3 in Appendix A, you would be committing mathematical suicide as the problem would be rendered unsolvable once "hour" is cancelled out.

Chapter 1 can be a useful supplement for students to read, but a more complete presentation of dimensional analysis should be given without closely following the material in this chapter.

Page 2: At the bottom, "Step I: Determining the Starting Factor and Answer Unit," should read, "Step I: Determining the Answer Unit." Determining the starting factor should come after Step II, since the starting factor is not always given, there can be more than one possible starting factor, and the best starting factor to use may be one of the conversion factors determined in Step II. Picking a starting factor from what you are given or know is the first step of Step III--setting up/solving the conversion equation.

Page 7: Emphasize that several of the equivalents in the table are fairly rough approximations. Give the actual equivalents--some students will want to know. Also, if the value of an equivalent can be 5% off, then, to be consistent, any test answer that is within +5% of the correct value should be counted correct. In some (unlikely) cases answers could be as much as 10% off when several approximate equivalents are used to compound the error.

Page 49: In the example at the bottom of the page you are given 25 mg/kg/24-hr (or day). The third unit given should not be dropped. There is a way to deal with problems of this type (25 mg/kg/day = 25 mg/kg x day) that can be consistently applied to all problems of this type. Triple unit factors are common and the difficulty they pose should be dealt with head on. All the various ad hoc attempts to get around these problems result in endless trouble in the long run. In this example the answer unit is given as "mL," whereas the correct answer unit is "mL/day." The problem should be setup as:

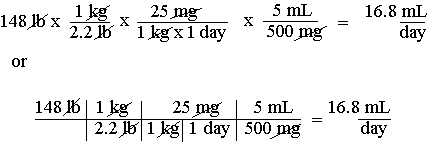
Whatever initial difficulty this technique may present for students not already familiar with it, it is still the technique of choice and will save a lot of grief later on. Some of the techniques contrived to deal with these problems work on some problems, but not others. The technique used above has the virture of working with all problems involving triple unit factors.

Page 50: In the two examples on this page the Answer Unit is incorrectly given as "cap" whereas "cap/dose" is what is really desired. In the first example, you are given 50 mg/kg/day and 4 doses/day, but not knowing what to do with "mg/kg/day" the problem is broken into two problems. The "day" is initially ignored, then brought back in the second part of the problem, thus paving the way for confusion and error. The logically consistent one-step setup would be:

For the second example the setup should be:

In the box at the bottom on the page are several warnings ("critically important," "easy to forget") that do not apply when the problems are done in a single step.

Page 105: Avoid the two-step technique, and ignore the two examples at the bottom of the page. Work out as above.

Page 160: Ignore examples. Omit the spurious "1 min" Starting Factors. Note that Answer Units are also wrong (should be "gtt/min," not just "gtt"). All that needs to be done is to cross out the "1 min" at the beginning of each example and add "/min" to "gtt" (the correct answer unit).

Pages 164, 165, and 166: Ignore these examples as above.

Pages 177, 178: Again, ignore the spurious Starting Factors and use the correct Answer Units for the last two examples on page 177, and examples 2 and 3 on page 178.

Pages 184, 185: Ignore examples. Another ad hoc variation in technique is introduced without comment in step 1 of the first example. Students will get into trouble if they try to extend this example to other problems. Also, what if the desired answer units were "mcg/hr?" Would students have trouble cancelling out "min" with "min" apparently on top? Putting "mcg/min" on top invites confusion. A better setup for step 1 would be:

For step 2:

For steps 3 and 4, just omit the "1 min."

Page 189, 190: Cross out the meaningless Starting Factors in examples 1, 3, 4, 5, and 6. In example 2, change "mcg/min" over "kg" to "mcg" over "kg x min."

Page 196: In Example a., the setup is in error due to a failure to fully label units. The 10 mL is "10 mL water." You have to ask, "10 mL of what?" Your answer unit is "mL Chloromycetin sol" and not just "mL." You can't use "mL water" and end up with "mL Chlor. sol." When you add 10 mL water to reconstitute you will end up with somewhat more than 10 mL Chlor. solution. Since you want "mL Chlor. sol" in your answer, pick a factor that has "mL Chlor. sol" in it and in the right place. You are given "100 mg/mL" which should be more completely written as "100 mg Chlor./mL Chlor. sol" and "10 mL/g" should be "10 mL water/1 g Chlor." which is quite an unnecessary bit of information for solving this problem, though the text incorrectly uses it (and by luck gets away with it). The correct setup should be:

Page 205: Omit spurious Starting Factors from example.

Page 220, 221: The first example asks, "How many mL should the child receive per dose?" The answer unit, therefore, should be "mL/dose" and not "mL." You are given 15 mcg/kg/dose, so solve as shown above for examples on pages 49 and 50--likewise with the second example on page 221.

Page 225: Again, example gives 50,000 U/kg/day and 4 doses/day, so a one-step setup would be:

That's about it. The other 96% of the text is okay.

This may be a case of a book being the worst textbook on dimensional analysis available--with the exception of all the others. I've heard that it is much better than its predecessor. Several medication math textbook titles are currently available, but not having reviewed them, I can't assume any do a better job, but I think other titles should be looked into.

There are errors of omission where students are not given a complete enough understanding of dimensional analysis to do all problems that could crop up. There are errors of commission where students are taught flawed or even erroneous technique. Throughout the textbook, overly simplified examples are used that fail to show the range of problems that students may encounter. A wider range of problems, however, would have illustrated the shortcomings of the techniques as taught, and appear to have been omitted for that reason.

Overall, however, I would say that this book is quite usable provided its shortcomings and flaws are amended. A better rounded, more robust presentation of dimensional analysis is definitely needed. Students should not only do well solving test problems, but come away feeling confident in their ability to handle any problems that may come their way in the future.