Conversion factors for nursing students.

The steps for doing dimensional analysis are given in the textbook as:

1. Determine the starting factor and answer unit.
2. Formulate a conversion equation.
3. Solve the conversion equation.

Determining the answer unit or units is crucial; they are not always obvious and can be challenging to determine. For some problems, reading the problem correctly is the only challenge. Students need to be able to translate sometimes convoluted English descriptions of a problem into clear, properly labeled factors they can later use to solve the problem. This skill is not emphasized in the textbook. If the answer unit is always given in the examples used, then this is because the examples have been contrived to be more simple and consistent than actual problems tend to be.

In some real-world problems no starting factor is given, or several possible starting factors are given with no way to decide, initially, which to use. It is preferable, in such cases, to determine everything you know that might be relevant to solving the problem, then decide, after the answer unit is determined, which of the factors you know would make an appropriate starting factor.

All examples used throughout the text use only numbers having a single unit attached for starting factors. Apparently "1 hour" is an acceptable starting unit, but "250 mL/hour" is not. This is not correct as starting factors are often in the form of "something per something." Indeed, some problems cannot be solved if they have a single unit starting factor (see example 3 in Appendix A).

While many conversion factors are approximations, and fraction of a percent errors are unimportant in medication math, 10 percent errors are a bit worrisome. Equating 1 grain with 60 milligrams when the actual equivalency is closer to 64.8 mg, is questionable, as is equating liters and quarts, or 1 mL to 15 minims (actually 1 mL = 16.23 minims). It is possible to solve a problem and come up with answers that differ by as much as 10% depending on which approximate conversion factors you decide to use. If + 5% errors are acceptable, then, as an aside, any answer to a test question that is within 5% of the correct answer should be counted as correct. It is oddly inconsistent to insist on carrying out calculations to two decimals, rounding to the nearest tenth, when far greater errors can be introduced by using loose approximations.

When, in chapter 6, a problem involving amount/body weigh/day comes up, the solution is presented in an unorthodox way. The problem (p. 49) gives 25 mg/kg/24 hr. When doing dimensional analysis it is essential that all the units given should be used and accounted for. Ignoring a given unit, then pulling it out of thin air at the end is poor technique, yet this is what the textbook does. The solution is given as:

The problem is that the correct answer units should be how many mL should be administered per day, or "mL/day." Omitting the "per day" part doesn't alter the fact that that is what you want to know—not per hour, not per dose, but per day. There is actually a simple rule that applies here. For example, when acceleration is measured in feet per second per second, it is not written as ft/sec/sec, but as ft/sec ² because ft/sec/sec is equal to ft/sec x sec. So if you're given mg/kg/day, the preferred way to deal with such a "triple decker" is to rewrite it as mg/kg x day. In this form it can be used, all undesired units cancel, and you end up with the desired answer with the right units attached:

If the problem called for "mL/dose" given 4 doses per day, then the solution is straightforward:

If "day" were omitted, however, this problem would become more difficult to solve. The textbook method is to calculate "mL," then divide by 4 to get "mL/dose." Students must remember to perform this final "critically important" step which would not exist if better technique were used. As the text acknowledges, "it is easy to forget to divide the total daily dose into the prescribed number of doses, thus greatly increasing the risk of administering an overdosage (sic)."

Problems of this sort are common, and it is unfortunate that the authors neglect to show students how to logically deal with them. The risk of confusing some students by introducing a new rule can hardly be worth the risk of error introduced by teaching a flawed technique.

In Chapter 10, page 184, an example is shown, as a model for students to follow, to determine how many mcg/min must be administered to a 215 lb patient at 3 mcg/kg/min:

In this example, at least, minutes are not omitted then added at the end, and the technique is not even erroneous, but merely confusing to many students and visually awkward. A student might try to logically extend this technique to determine mL/hr:

The student who notices that the answer doesn't make sense might wonder what went wrong. Would they realize that when "mcg" was cancelled that "3 1/min" was left requiring the use of 60 min/1 hr instead of 1 hr/60 min? Trying to explain how to work around the poor technique employed by this example only digs a deeper hole. The better response to student confusion would be to have them put a big X mark over this section of the textbook and show them a sensible way to set it up:

Another case of flawed technique arises in Chapter 10. Students are given problems that require converting from mL/hr to gtt/min, and are shown conversion equations like the following:

The problem, again, is that the correct answer unit is "gtt/min" and not "gtt" as it appears. The correct answer is just pulled out of nowhere and declared to be "33 gtt/min." The initial starting factor of "1 min" is spurious. It is not a given, and it means absolutely nothing to say that you know "1 min" or "1 hour" or "1 cabbage." If such meaningless starting factors are simply omitted from such examples, the problems are perfectly setup to yield the correct answers with the correct answer units. It seems that the pseudo-starting factor is used to avoid having a starting factor with more than one unit attached. As mentioned, however, there is no such requirement when doing dimension analysis. In the above example "90 mL/1 hr" would make a logical and perfectly good starting factor.

Students should be told to just ignore the nonsensical "1 min" and "1 hour" starting factors. If you were to introduce "1 hour" as a starting factor in example 3 in Appendix A, you would be committing mathematical suicide as the problem would be rendered unsolvable once "hour" is cancelled out.

Here's an actual example from chapter 10:

Calculation of IV Flow Rate When Total Infusion Time is Specified

Order: 1000 mL of D5W (5% Dextrose in water) IV to infuse over a period of 5 hr

Drop Factor: 10 gtt/mL

Starting Factor Answer Unit

1 min gtt (drops)

Equivalents: 1000 mL = 5 hr, 10 gtt = 1 mL, 60 min = 1 hr

Conversion Equation:

1 min x 1 hr x 1000 mL x 10 gtt = 33.3 = 33 gtt
60 min 5 hr 1 mL

Flow Rate: 33 gtt/min

For review, let's go over this problem.

1. There are two errors relating to the starting factor. One is procedural—there is no logical way to pick a starting factor as the first step. The other is that "1 min" is a meaningless factor. I can meaningfully say that I know there are 10 drops per mL, but it means nothing to say that I know "1 min" in the context of this problem.

2. The answer unit is wrong. I want to know a rate of flow in drops per some unit of time. Just "gtt" doesn't cut it.

3. Factors are expressed as equalities. It should read "something per something" and not "something equals something" which leads to absurd statements like "25 mg = 1 kg"

4. By introducing a spurious starting factor the setup is in error, as is the resultant answer. The number is correct, but the answer unit is not.

5. The final statement, that the flow rate is 33 gtt/min, is the only part of the example that is correct, but it is logically disconnected from everything that precedes it.

So, let's see, the text manages to state an incorrect answer unit, then introduces a spurious starting factor, which makes the setup wrong, which yields 33 gtt for an answer, which is also wrong. But through some sort of mental slight-of-mind, they finally come up with the correct answer, which they simply declare to be 33 gtt/min.

Is there a better way to do this problem? First ask, what do I want to know? The flow rate in gtt/min, which is my answer unit, not just gtt (drops). What do I know? I'm given that there are 10 gtt/mL and that the infusion rate is 1000 mL/5 hr. Since I want gtt on top and 10 gtt/mL has gtt in the right place, 10 gtt/mL makes a perfectly good starting factor—I just need to get from mL to min. My set up then:

10 gtt x 1000 mL x 1 hr = 33 gtt
1 mL 5 hr 60 min min

Just omitting the "1 min" from the textbook's setup would also work.

As to what the authors might be thinking, the only clue to their reasoning was given in the following paragraph that preceded this example:

"In calculating the flow rate for drops per minute , one minute becomes the labeled value that must be converted to an equivalent value: number of drops. One minute , therefore, is the starting factor and drops is the answer unit and these, as in all dimensional analysis conversions, form an equivalent relationship."

On page 9 is the following table:

Table 1-2 Conversion Equation

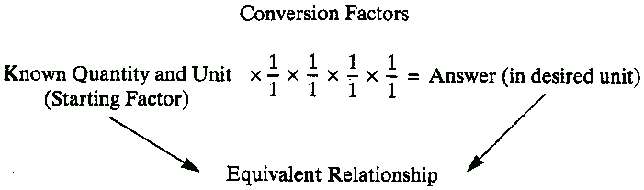
This table reveals how the authors think about dimensional analysis. They see the starting factor as something given; there can be only one starting factor; it has only one unit associated with it, and it forms a special "equivalent relationship" with the answer unit, which, being equivalent, must also have only a single unit associated with it. In between are conversion factors that are fundamentally different from the starting factor.

All of these assumptions are incorrect as generalizations about dimensional analysis. The only equivalent relationship is between what is on the left side of the equal sign and what is on the right side. One could speak of an equivalent relationship between the "numerator" and "denominator" of a conversion factor (2.2 lb/1 kg means 2.2 lb = 1 kg), but otherwise there is no necessary "equivalent relationship" implied.

There is a particular type of DA problem, the simple conversion problem, that does involve going from one unit of measure to another equivalent measure (such as converting from feet to meters). In this subtype of problem you have only one logical starting factor, which can be said to be equivalent to your answer (10 inches x 2.54 cm/1 inch = 25.4 cm), but such problems should not be taken as a model for all DA problems, which appears to be what has happened.

By the Commutative Law of Multiplication, it doesn't matter what order the factors on the left side are multiplied in. Therefore any factor could be first, and thus be the starting factor, although usually only one or two factors qualify to be thought of as logical starting factors. Both starting factors and answer units are often in the form of something per something. You could start with miles/hour and end up with seconds in your answer, for example, without any equivalence between starting factor and answer unit.

It appears that such fundamental misunderstandings underlie the errors in the textbook. Problems that do not conform to their notions are tortured into compliance by introducing spurious starting factors and using obviously incorrect answer units. I don't think it is going too far to suggest that the poor technique exhibited by the textbook makes it difficult for students to master med-math. Indeed, those who do must do so in spite of the textbook and not because of it.

Recommended Corrections to:

Clinical Calculations: A unified approach (4th ed.)

Chapter 1 can be a useful supplement for students to read, but a more complete presentation of dimensional analysis should be given without closely following the material in this chapter.

Page 1: A Google search shows that only this textbook and a few nursing sites associate "label factor" with dimensional analysis (DA). Likewise "unit conversion" is not a synonym for DA. The only synonym commonly used is "factor-label method." While this point is nit-picky, I would expect the authors to use the same terminology as everyone else by the 4th edition.

Page 2: At the bottom, "Step I: Determining the Starting Factor and Answer Unit," should read, "Step I: Determining the Answer Unit." Determining the starting factor should come after Step II, since the starting factor is not always given, there can be more than one possible starting factor, and the best starting factor to use may be one of the factors determined in Step II. Picking a starting factor from what you are given or know is the first step of Step III—setting up/solving the conversion equation.

Page 4: In the box is the statement: "When the conversion equation is solved, it will be seen that the starting factor and the labeled answer have formed an equivalent relationship." The belief that this is true leads to serious error and confusion in Chapter 10. If true, the collorilary would be that if the starting factor has one unit of measure associated with it, then the answer unit can have only one unit of measure associated with it and vice versa .

Page 7: Emphasize that several of the equivalents in the table are fairly rough approximations. Give the actual equivalents—some students will want to know. Also, if the value of an equivalent can be 5% off, then, to be consistent, any test answer that is within + 5% of the correct value should be counted correct. In some (unlikely) cases answers could be as much as 10% off when several approximate equivalents are used to compound the error.

Page 49: In the example at the bottom of the page you are given 25 mg/kg/24-hr (or day). The third unit given should not be dropped. There is a way to deal with problems of this type (25 mg/kg/day = 25 mg/kg-day) that can be consistently applied to all problems of this type. Triple unit factors are common and the difficulty they pose should be dealt with head on. All the various ad hoc attempts to get around these problems result in endless trouble in the long run. In this example the answer unit is given as "mL," whereas the correct answer unit is "mL/day." The problem should be setup as:

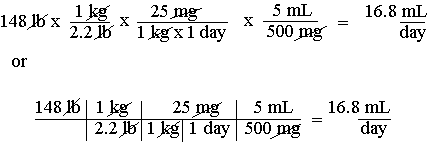
Whatever initial difficulty this technique may present for students not already familiar with it, it is still the technique of choice and will save a lot of grief later on. Some of the techniques contrived to deal with these problems work on some problems, but not others. The technique used above has the virtue of working with all problems involving triple unit factors.

Page 50: In the two examples on this page the Answer Unit is incorrectly given as "cap" whereas "cap/dose" is what is really desired. In the first example, you are given 50 mg/kg/day and 4 doses/day, but not knowing what to do with "mg/kg/day" the problem is broken into two problems. The "day" is initially ignored, then brought back in the second part of the problem, thus paving the way for confusion and error. The logically consistent one-step setup would be:

For the second example the setup should be:

In the box at the bottom on the page are several warnings ("critically important," "easy to forget") that do not apply when the problems are done in a single step.

Page 105: Avoid the two-step technique, and ignore the two examples at the bottom of the page. Work out as above.

Page 159: Cross out the second paragraph: "In calculating the flow rate for drops per minute , one minute becomes the labeled value that must be converted to an equivalent value: number of drops. One minute , therefore, is the starting factor and drops is the answer unit and these, as in all dimensional analysis conversions, form an equivalent relationship."

Page 160: Ignore examples. Omit the spurious "1 min" Starting Factors. Note that Answer Units are also wrong (should be "gtt/min," not just "gtt"). All that needs to be done is to cross out the "1 min" at the beginning of each example and add "/min" to "gtt" (to get the correct answer unit).

Pages 164, 165, and 166: Ignore these examples as above.

Pages 177, 178: Again, ignore the spurious Starting Factors and use the correct Answer Units for the last two examples on page 177, and examples 2 and 3 on page 178.

Pages 184, 185: Ignore examples. Another ad hoc variation in technique is introduced without comment in step 1 of the first example. Students will get into trouble if they try to extend this example to other problems. Also, what if the desired answer units were "mcg/hr?" Would students have trouble canceling out "min" with "min" apparently on top? Putting "mcg/min" on top invites confusion. A better setup for step 1 would be:

For step 2:

For steps 3 and 4, just omit the "1 min." and "1 gtt"

Page 189, 190: Cross out the meaningless Starting Factors in examples 1, 3, 4, 5, and 6. In example 2, change "mcg/min" over "kg" to "mcg" over "kg x min."

Page 196: In Example a., the setup is in error due to a failure to fully label units. The 10 mL is "10 mL water." You have to ask, "10 mL of what?" Your answer unit is "mL Chloromycetin sol" and not just "mL." You can't use "mL water" and end up with "mL Chlor. sol." When you add 10 mL water to reconstitute you will end up with somewhat more than 10 mL Chlor. solution. Since you want "mL Chlor. sol" in your answer, pick a factor that has "mL Chlor. sol" in it and in the right place. You are given "100 mg/mL" which should be more completely written as "100 mg Chlor./mL Chlor. sol" and "10 mL/g" should be "10 mL water/1 g Chlor." which is quite an unnecessary bit of information for solving this problem, though the text incorrectly uses it (and by luck gets away with it). The correct setup should be:

Page 205: Omit spurious Starting Factors from example.

Page 220, 221: The first example asks, "How many mL should the child receive per dose?" The answer unit, therefore, should be "mL/dose" and not "mL." You are given 15 mcg/kg/dose, so solve as shown above for examples on pages 49 and 50—likewise with the second example on page 221.

Page 225: Again, example gives 50,000 U/kg/day and 4 doses/day, so a one-step setup would be:

That's about it. The other 96% of the text is okay.

Textbook Guide to Dimensional Analysis

(as compiled from various pages throughout the textbook)

Determine the starting factor* and answer unit.

Initially, it is essential to determine exactly what information is sought: the known quantity called the starting factor , and the desired unit to which the starting factor will be converted, the answer unit.

When the conversion equation is solved, it will be seen that the starting factor and the labeled answer have formed an equivalent relationship.

In calculating the flow rate for drops per minute (or mL per hour) one minute (or one hour) becomes the labeled value that must be converted to an equivalent value: number of drops (or mL). One minute , therefore, is the starting factor and drops is the answer unit and these, as in all dimensional analysis conversions, form an equivalent relationship.

Formulate a conversion equation consisting of a sequence of labeled factors, in which successive units can be cancelled until the desired answer unit is reached.

If a given is in the form mg/kg/day, ignore the third unit, do the conversion, then remember to factor the omitted unit back in. If in the form mcg/kg/min, change to mcg/min over kg if mcg/min is the answer unit.

If a percentage is given, e.g. 25%, rewrite as 25/100 with appropriate labels.

Determine conversion factors that may be needed. You will need enough to form a "bridge" to your answer unit(s).

Use only conversion factors that have a 1:1 relationship

It is desirable that conversion factors be arranged in a sequence so that identical units are placed diagonally.

In setting up the conversion factors, it is helpful to write the denominator first, as this contains the unit of the preceding numerator and facilitates cancellation of successive units.

Solve the conversion equation by use of cancellation and simple arithmetic.

Cancel units first

Reduce numbers to lowest terms.

Multiply/divide to solve the equation.

Reduce answer to lowest terms, convert to decimal, and/or round off.

Take a few seconds and ask yourself if the answer you came up with makes sense. If it doesn't, start over.

* The text in red represents weak or erroneous technique. Errors of omission are not indicated.

Conclusions

This may be a case of a book being the worst textbook on dimensional analysis available—with the exception of all the others. I've heard that it is much better than its predecessor. Several medication math textbook titles are currently available, but not having reviewed them, I can't assume any do a better job, but I think other titles should be looked into.

There are errors of omission where students are not given a complete enough understanding of dimensional analysis to do all problems that could crop up. There are errors of commission where students are taught flawed or even erroneous technique. Throughout the textbook, overly simplified examples are used that fail to show the range of problems that students may encounter. A wider range of problems, however, would have illustrated the shortcomings of the techniques as taught, and may have been omitted for that reason.

Overall, however, I would say that this book is quite useable provided its shortcomings and flaws are amended. A better rounded, more robust presentation of dimensional analysis is definitely needed. Students should not only do well solving test problems, but come away feeling confident in their ability to handle any problems that may come their way in the future.

Visit our Zazzle store:

Fine Poster Art

Support this site: Visit our Zazzle store featuring ultra hi-res images of artworks, Hubble/ESA/NASA space images, Mandelbrot fractals, maps and more. Images up to 525 megapixels allow for fine printing at the largest sizes. Give a fine print as a gift that could hang around for a hundred years.