Dimensional analysis (also known as the factor-label method or unit-factor method) is by far the most useful math trick you'll ever learn. Maybe you've learned some algebra, but will you use it? For many people the answer is, "not after the final exam."

For a fraction of the effort needed to learn algebra, you too can learn "dimensional analysis." First off, however, let's get rid of the big words. What this is all about is just conversion—converting one thing to another. This is something you will have occasion to do in real life. This is seriously useful stuff.

This trick is about applied math, not about numbers in the abstract. We're talking about measurable stuff, stuff you can count. Anything you measure will have a number with some sort of "unit of measure" (the dimension) attached. A unit could be miles, gallons, miles per second, peas per pod, or pizza slices per person.

Example 1

 
How many seconds are in a day?

First, don't panic. If you have no idea what the answer is or how to come up with an answer, that's fine—you're not supposed to know. You're not going to solve THE PROBLEM. What you are going to do is break the problem down into several small problems that you can solve.

Here's your first problem:

1. Ask yourself, "What units of measure do I want to know or have in the answer?" In this problem you want to know "seconds in a day." After you figure out what units you want to know, translate the English into Math. Math is a sort of shorthand language for writing about numbers of things. If you can rephrase what you want to know using the word "per," which means "divided by," then that's a step in the right direction, so rephrase "seconds in a day" to "seconds per day." In math terms, what you want to know is:

2. Ask, "What do I know?" What do you know about how "seconds" or "days" relate to other units of time measure? You know that there are 60 seconds in a minute. You also know that in 1 minute there are 60 seconds. These are two ways of saying the same thing. You know that there are 24 hours in a day (and in one day there are 24 hours). If you could now connect "hours" and "minutes" together you would have a sort of bridge that would connect "seconds" to "days" (seconds to minutes to hours to days). The connection you need, of course, is that there are 60 minutes in an hour (and in one hour there are 60 minutes). When you have this kind of connection between units, then you know enough to solve the problem--but first translate what you know into math terms that you can use when solving the problem. If in doubt, write it out:

All of these statements, or conversion factors, are true or equivalent (60 seconds = 1 minute). All you need to do now is pick from these statements the ones that you actually need for this problem, so....


3. Ask, "From all the factors I know, what do I need to know?"

Remember that you want to know:

So pick from the things you know a factor that has seconds on top or day(s) on the bottom. You could pick either of the following two factors as your "starting factor:"

Write down your starting factor (say you pick 60 seconds per 1 minute):

Now the trick is to pick from the other things you know another factor that will cancel out the unit you don't want. You start with "seconds" on top. You want "seconds" on top in your answer, so forget about the seconds—they're okay. The problem is you have "minutes" on the bottom but you want "days." You need to get rid of the minutes. You cancel minutes out by picking a factor that has minutes on top. With minutes on top and bottom, the minutes will cancel out. So you need to pick 60 minutes per 1 hour as the next factor because it has minutes on top:

You now have seconds per hour, since the minutes have cancelled out, but you want seconds per day, so you need to pick a factor that cancels out hours:

4. Solve it. When you have cancelled out the units you don't want and are left only with the units you do want, then you know it's time to multiply all the top numbers together, and divide by all the bottom numbers.

In this case you just need to multiple 60x60x24 to get the answer: There are 86,400 seconds in a day.

Here's how this problem might look if it were written on a chalkboard:

 

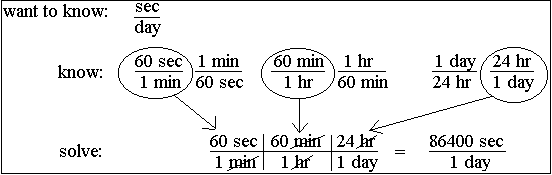
Remember that you don't need to worry about the actual numbers until the very end. Just focus on the units. Plug in conversion factors that cancel out the units you don't want until you end up with the units you do want. Only then do you need to worry about doing the arithmetic. If you set up the bridge so the units work out, then, unless you push the wrong button on your calculator, you WILL get the right answer every time.

Example 2

How many hours are in a year?

Let's go through the steps:

Don't panic

What do you want to know? This one's easy: hours in a year, or better, hours per year

Translate into math terms:

What do you know that you might need to use? You know that there are 24 hours in a day, 7 days in a week, 4 weeks in a month, 12 months in a year, and about 365 days in a year. The converse, of course, is also true: In one day there are 24 hours, in one week there are 7 days, in one month there are 4 weeks, in one year there are 12 months, and in one year there is about 365 days (actually closer to 365.25 days).

Translate into math terms—writing them all down can't hurt:

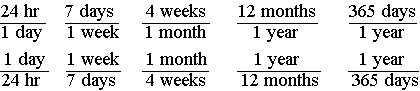
Pick a starting factor. Since you want hours on top (or years on the bottom), you could start with 24 hours per day:

Now pick whatever factors you need to cancel out day(s):

Keep picking factors that cancel out what you don't want until you end up with the units you do want:

 

Do the math. You have all the units cancelled out except hours per year, which is what you want, so when you do the math, you know you'll get the right answer:

But wait, why not go from "hours" to "year" using the fact that there are 365 days per year?

Oh no! There is a 696-hour difference between the two answers! How can this be? Exact answers can only be obtained if you use conversion factors that are exactly correct. In this case there are actually more than 4 weeks in a month (about 4.35 weeks per month). Since there is a bit more than 365 days in a year (365.25 days), a more accurate answer still, to the nearest hour, would be that there are 8766 hours in a year. The point of this example is that your answer can only be as accurate as the conversion factors you use.

Example 3

Sometimes both the top and bottom units need to be converted:

If you are going 50 miles per hour, how many feet per second are you traveling?

If you were to do this one on the blackboard, it might look something like this:

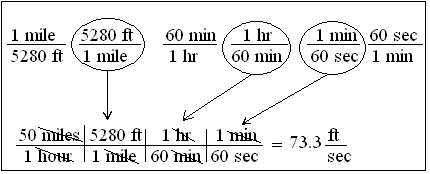
You want your answer to be in feet per second. You are given 50 miles per hour. Notice that both are in distance per time. Normally you can use any value given by the problem as your starting factor. One thing you know, then, is given. The other things you just know or have to look up in a conversion table. Although every conversion factor can be written two ways, you really only need to write each one way. That's because you know you can always just flip it over and then use it. If you have written 60 min/1 hr, then to solve this problem you would just flip the 60 min/hour factor over. With practice you won't even need to write down what you know, you'll just pull it out of your head and write down the last part, do the math, and get the right answer.

Example 4

How much bleach would you need to make a quart of 5 percent bleach solution?

You're not told what answer unit to use, but ounces would work since there are 32 oz in a quart. If the only thing you had to measure bleach with was in milliliters, then you would pick "mL" as your answer unit.

When you are given something like "5 percent" or "5%" by a problem, you need to translate it into math terms you can use. "5%" means 5 per 100 or 5/100, but 5 what? per 100 what? You need to label the numbers appropriately. In this example you write down "5 oz bleach/100 oz bleach solution" or just "5 oz B/100 oz BS" as a factor you are given. If you were going for milliliters, then you would use "5 mL B/100 mL BS." The top and bottom units must be the same or equivalent, but otherwise can be any units you may need. If you had 5 gal. bleach/100 gal. bleach solution, then you would still have a 5% bleach solution.

Setting up and solving this problem is now easy:

So you would add 1.6 oz bleach to a quart measuring cup, then add water (30.4 oz) to make 32 ounces of 5% bleach solution.

 

Example 5

Your little sister's hamster is slowly dying a horrable death from multiple tumors and has stopped eatting. The vet wants $75 to put it to sleep. It is Friday night and even if Mom was willing to spend $75 the hamster and your sister would have to suffer until Monday. You look online and find information about small animal euthanasia. It says you need some vinegar or other 5% acid solution. There is no vinegar in the house, only some muraitic swimming pool acid in the garage. Instead of waiting until tomorrow to go to town and buy vinegar, you want to do something now. According to the label it is 31.45% hydrochloric acid (HCl). Realizing it is dangerous to mess with hydrodhloric acid, you take precautions you learned in chemistry class. Also from chemisty class you recall there is a formula, something about V2 times C2 over C1 but this is not a test, this is for real, and getting the wrong answer is not an option. Fortunately, also in chemistry, you learned dimentional analysis and know that if the formula (and answer) is correct, the units of measure will cancel out leaving you with only the ones appropriate for the answer. So you stop trying to recall the formula and decide to use DA. You have told your sister you can help Fuzzy go to sleep and stop thrashing about. She is crying and won't go to bed. She stares hopefully at you. She trusts you. You realize it is up to you now to not mess up.

So what you want to know is the number of ounces of concentrated (32%) HCl you need to use to make, say, a quart of 5% dilute acid solution. In the previous example involving bleach, the assumption was that the initial bleach solution was 100% bleach. But HCl doesn't come in a 100% acid form and what you have is about 32% acid. This means that in 100 oz. of concentrated HCl solution there are 31.45 oz. of actual HCl. You also know that in a 5% dilute solution there are 5 oz. actual pure HCl in 100 oz. of dilute solution. Since you want to end up with a quart of solution, you'll need to know that there are 32 oz/qt.

So how much of the concentrated acid do you need to use to make a quart of dilute 5% acid? In your answer you want concentrated on top and dilute on bottom, so start with dilute on bottom or concentrated on top:

If the volume of concentrated acid is V1 and its concentration is C1, and V2 is the dilute volume and C2 is the concentration of the dilute acid, then V1 = (V2xC2)/C1. You might remember this formula for a test, but don't expect to remember it when you need it. With dimensional analysis you can always think your way to the right answer. But knowing the right answer is not enough. You should also know not to ever add water to concentrated acid. So to make a quart of dilute acid you measure out 27 oz of water and add 5 oz concentrated acid to it. Following the instructions of the euthanasia site, Fuzzy goes quietly to sleep. This example is a real world one. Knowing some math can make all the difference.

 

Example 6

Your car's gas tank holds 18.6 gallons and is one quarter full. Your car gets 16 miles/gal. You see a sign saying, "Next gas 73 miles." Your often-wrong brother, who is driving, is sure you'll make it without running out of gas. You're not so sure and do some quick figuring:

"Ah! I knew I was right," declares your brother on glancing at your calculator,
"your calculations prove it!" Is this a good time to be assertive and demand that he turn around to get gas, or do you conclude that your brother is right for once?

Unless the next stop is Las Vegas and you're feeling really lucky, you should turn around and get some more gas. Your calculator reads "74.4" exactly, but if you believe what it says, then you believe that when the car runs out of gas, it will have gone some where between 74.35 miles and 74.45 miles or 74.4 + 0.05 miles. Obviously the "point four" is meaningless, so you round to 74. Is 74 the right answer? If you think it is, then you think your car will go some where between 73.5 miles and 74.5 miles before running out of gas. When you run out of gas, what chance do you think you'll have of having gone 74 + 0.5 miles? A proverbial "fat chance" would be a good guess.

When you're given something like a "quarter tank" you should wonder just how accurate such a measurement is. Can you really divide 18.6 by 4 and conclude that there really is 4.65 gallons of gas in the tank? The last time you figured mileage you came up with 16 miles/gallon, but is the engine still operating as efficiently? Are the tires still properly inflated? Will the next 73 miles be uphill? Do you have a head wind? Surely a calculated estimate of 74 miles is overly precise. A realistic answer, then, might be 74 + 10 miles. You realize you could run out of gas anywhere between 66 and 84 miles, so you finally and correctly conclude that you have a slightly less than a 50/50 chance of running out of gas before reaching the next gas station.

The point of this example is to remind you that dimensional analysis is applied math, not abstract math. The numbers used should describe the real world in so far as possible and indicate no more accuracy than is appropriate. If you overlook this point, you might have a five-mile walk to the next gas station.

Example 7

You're throwing a pizza party for 15 and figure each person might eat 4 slices. How much is the pizza going to cost you? You call up the pizza place and learn that each pizza will cost you $14.78 and will be cut into 12 slices. You tell them you'll call back. Do you have enough money? Here's how you figure it out, step by step.

1. Ask yourself, "What do I want to know?" In this case, how much money is the pizza going to cost you, which in math terms is: cost (in dollars) per party, or just $/party. This is your "answer unit." This is what you are looking for.

2. Ask, "What do I know?" Write it all down, everything you know: one pizza will cost you $14.78 (in math terms 1 pizza/$14.78). You also know that for $14.78 you can buy one pizza ($14.78/1 pizza). It can be important to realize that every conversion factor you know can be written two ways. One of these ways may be needed to solve the problem and the other won't, but in the beginning you don't know which, so just write them both ways. Continue writing down other things you know. You know, or hope, that only 15 people will be eating pizza (15 persons/1 party), or for this one party, 15 people will come (1 party/15 persons). You also know there will be 12 slices per pizza (12 slices/1 pizza), or that each pizza has 12 slices (1 pizza/12 slices). The last thing you know is that each person gets 4 slices (1 person/4 slices), or that you are buying 4 slices per person (4 slices/person). Math is a language that is much briefer and clearer than English, so writing every thing you know in math terms, here's what you might have written down:

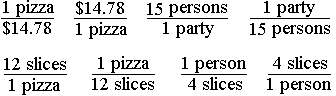
3. Ask, "From all the things above I know, what do I actually need to know to figure out the problem?"

Remember that you want to know $/party, so pick one of the things you know that has either dollars on top, or "party" on the bottom. Let's start with $14.78/pizza as the starting factor. Great, you got dollars on top, but "pizza" on the bottom where you want "party." To get rid of "pizza" pick one of the things you know that has "pizza" on the top. "Pizza" over "pizza" cancels out, so you get rid of the "pizza:"

Okay, you now have dollars per slice, but you want dollars per party, so now what? Easy, just keep picking from the things you know whatever cancels out the units you don't want. The numbers go with the units, but don't worry about numbers, just pay attention to the units. So you pick 4 slices/1 person to get rid of "slices," then 15 persons/1 party to get rid of "person(s):"

Now multiply all the top numbers, and then divide by any bottom numbers to get the right number. Finally add the units that are left over to the number to get the answer you wanted. Using this method, you can hardly go wrong unless you push the wrong button on your calculator.

By the way, how many pizzas should you order? Figuring this out should be as easy as....

Example 8

Chemists often use dimensional analysis. Here's a chemistry problem. To solve it you need to know that, as always, there are 6.02 x 10²³ molecules (or atoms) of whatever in a mole.

A sample of calcium nitrate, Ca(NO₃)₂, with a formula weight of 164 g/mol, has 5.00 x 10²⁵ atoms of oxygen. How many kilograms of Ca(NO₃)₂ are present?

This may look like a some sort of horribly complex nightmare problem, but don't panic, just take it step by step. Since you want kilograms (kg) in your answer, pick a starting factor with weight (g=grams) on top. Note that in each molecule of calcium nitrate there are two nitrate ions each having three atoms of oxygen (for a total of 6).

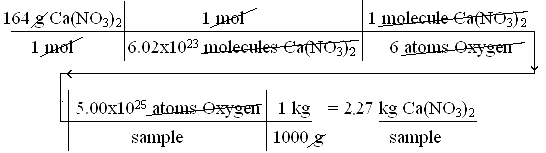
Example 9

You have come down with a bad case of the geebies, but fortunately your grandmother knows how to cure the geebies. She sends you an eyedropper bottle labeled:

Take 1 drop per 10 lbs. of body weight per day divided into 4 doses until the geebies are gone.

This problem is a bit more challenging, but don't panic. Break the problem down into a bunch of small problems, and tackle each one by one.

What do you want to know? In order to take one dose 4 times a day you need to know how many drops to take per dose.

Translated into math terms you want the answer to be in:

What do you know? Well, you know you weigh 160 pounds. You know that you need to take 4 doses per day (implied). You know that you need to take 1 drop per 10-lbs. body weight per day.

Translate this into math terms:

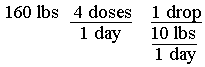
The problem now is the last factor. What can you do with such an odd factor? You rewrite it so it is in a different form that you can use. What you do is multiply the middle term by the bottom term:

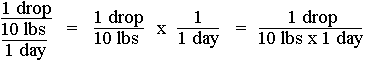
So whenever you have a triple-decker, use this trick to rewrite the factor.

Now you should be able to solve the problem. The one thing you know that isn't a conversion factor is that you weigh 160 lbs., so use that as your starting factor:

If you had wanted to know how many drops per day to take, you would have just left off the last conversion factor, which would give you an answer of 16 drops/day.

Example 10

Okay, enough easy problems, let's try something harder. Well, not really harder, just longer. The point of this example is that no matter how ridiculously long your conversion might be, long problems are not really more difficult. If you get the point, then skip this example; otherwise read on.

At the pizza party you and two friends decide to go to Mexico City from El Paso, TX where y'all live. You volunteer your car if everyone chips in for gas. Someone asks how much the gas will cost per person on a round trip. Your first step is to call your smarter brother to see if he'll figure it out for you. Naturally he's too busy to bother, but he does tell you that it is 2015 km to Mexico City, there's 11 cents to the peso, and gas costs 5.8 pesos per liter in Mexico. You know your car gets 21 miles to the gallon, but we still don't have a clue as to how much the trip is going to cost (in dollars) each person in gas ($/person).

1. What do you want to know? $/person round trip—the answer unit(s).

2. What do you know so far? There will be 3 persons going on a round trip (3 persons/1 round trip), or in the planned round trip 3 persons will be going (1 round trip/3 persons), it will be a 2015 km trip one-way (2015 km/one-way trip), or one-way is 2015 km (one-way trip/2015 km), there are 2 one-way trips per round trip (2 one-way/round trip), there is 11 cents per peso (11 cents/1 peso), or one peso is worth 11 cents (1 peso/11 cents). Finally you know that one liter of gas costs 5.8 pesos (1 liter/ 5.8 pesos), or 5.8 pesos will buy you 1 liter (5.8 pesos/1 liter).

You know a lot, but still not enough. Knowing the number of miles in a kilometer, or liters in a gallon would be nice, but one of your friends recalls that there is 39.37 inches in a meter and the other is sure that there is 4.9 ml in a teaspoon. This still isn't enough. You might need to know that there are 1000 meters in a kilometer, 1000 ml in a liter, 100 cents per dollar, 12 inches to the foot, and 5,280 feet to the mile, but then you already knew that.

Almost enough, but how can you get from teaspoons to gallons? Simple, call your mom. She knows that there are 3 teaspoons in a tablespoon, 16 tablespoons in a cup, 2 cups in a pint, 2 pints in a quart, and 4 quarts in a gallon. Wow, that's a lot of things to know, but it should be enough. Write it all down in math terms and see what you have:

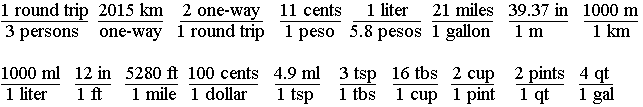
3. What do you need to know from the above? If any of the above are upside down from what you end up needing, just turn them over, then use them. This problem looks harder than it is. Since we want to end up with $/person, let's start with:

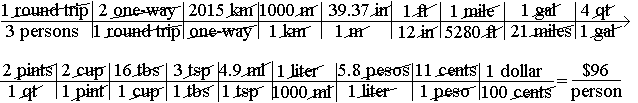
Even with 18 factors to plug in to get your answer, it's still pretty much a no-brainer whether you have two or 30 factors. If you know enough conversion factors and set the "bridge" up correctly to cancel out all unwanted units, then you get the correct answer. You may have to look up a few conversion factors you don't know, but once you do, you're home free. Looking up the number of liters per gallon or miles in a kilometer would have saved quite a few steps, but if you can remember any relationship you can still figure out your answer. It takes a little longer, but really adds nothing to the inherent difficulty. 

Example 11

Now this one is a bit hard if you haven't paid close attention to the previous examples.

You have come down with a bad case of the geebies, but fortunately your grandmother has a sure cure. She gives you an eyedropper bottle labeled:

Take 1 drop per 15 lb of body weight per dose four times a day until the geebies are gone. Contains gr 8 heebie bark per dr 100 solvent. 60 drops=1 tsp.

You weigh 128 lb, and the 4-oz bottle is half-full. You test the eyedropper and find there are actually 64 drops in a teaspoon. You are going on a three-week trip and are deeply concerned that you might run out of granny's geebie tonic. Do you need to see her before leaving to get a refill?

Try working this one out before reading further.

First, what do you want to know? You want to know how long the bottle will last. You could figure out days/bottle or weeks/bottle and see if the bottle will last longer than 3 weeks or 21 days. So you write down "days/bottle" as the units you want in your answer.

What do you know to start off with that you might need to know? You write down the following:

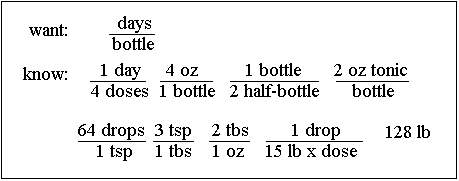
You realize that if a 4-oz bottle is half-full, then there is 2 oz of tonic in it, but you could figure it out dimensionally if you wanted to:

You would then end up with "days/half-bottle" in your answer, but it's easier to just go with 2 oz/bottle as you're given.

What should you use as a starting factor? You pick 128 lb because it's something you're given and it seems lonely. You set the problem up:

Houston, we have a problem. You ended up with units reversed from what you wanted. You figured out how much of the bottle you would use in one day. What to do? You could hit the 1/x button on your calculator if it had one, or invert the answer by dividing 1 by 0.044, or start over with 128 lb on the bottom. What? Can you do that? Sure you can. You could even put 128 lb on the end and on the bottom, or put it in the middle somewhere. You decide to start over, this time picking a starting factor that already has "day" or "bottle" in the right place.

So, it looks like you'll have enough. At some point you need to know how many drops per dose you will need to take, so you figure it out:

As a practical matter, you can't take 8.533 drops per dose; you have to round off. At this point you realize that when you calculated 22.5 days/bottle, you were not figuring on 9 drops/dose. You decide to recalculate to see if rounding up to 9 makes a significant difference.

You note a small difference, but conclude that you have just enough geebie tonic. Concluding that you have enough, however, and having enough may not be the same thing. The story continues:

You leave on your trip and on the 19th day you run out of geebie juice. You didn't spill any, and no one took any. You sit in a stunned stupor trying to figure out where you went wrong in your calculations.

You finally realize there might not have been 2.0 oz of tonic in the bottle to begin with. A measurement like "half a bottle" should not inspire great certainty. You wish you had measured the amount and found that the bottle contained 2.0 + 0.05 oz of tonic, but what you were given, more or less, was that you had 2 + 0.5 oz of tonic. There could be anything from 1.5 to 2.5 oz in the bottle. Recalculating using the low and high values, you find you had enough tonic to last somewhere between 16 and 26 days. If you had figured out the correct answer of 21 + 5 days the first time, you would have realized you had only slightly less than a 50/50 chance of running out, and would have gone to see Granny for a refill.

Summary

Don't panic.

Figure out what answer unit(s) you want to end up with. This is usually easy.

Write down, in math terms, everything you know that relates to the problem. You may need to read the problem several times, rephrasing parts of it, so you can translate everything into math terms. You may need to look up a few conversion factors, but that's inconvenient, not difficult.

Pick a starting factor. If possible pick one that already has one of the units you want in the right place. Otherwise start with something you are given that is not a conversion factor.

Plug in conversion factors that allow you to cancel out any units you don't want until you are left with only the units you do want (your answer units).

If you can't solve the problem, pick a different starting factor and start over.

Do the math. You may be less apt to make an error if you first multiply all the top numbers, then divide by all the bottom numbers. Now double-check your calculations. If you make a mistake it will probably be in hitting the wrong key on the calculator.

Ask yourself if the answer seems right or reasonable. If not, recheck everything.

A Step by Step Guide to Dimensional Analysis

The following summary can be used as a guide for doing DA. Some familiarity with DA is assumed. See above for an introduction to DA. While not all steps listed below will be needed to solve all problems, I have found that any problem that can be solved using DA will yield its answer if the following steps are followed. I would not suggest memorizing the sequence of steps, but rather understanding and practicing them. Understanding is more durable than memory.

1. Determine what you want to know. Read the problem and identify what you're being asked to figure
     out, e.g. "how many milligrams are in a liter of solution."
     a. Rephrase if necessary using "per." Example: You want to know "milligrams per liter."
     b. Translate into "math terms" using appropriate abbreviations to end up with "mg/L" as your answer
          unit (AU). Write this down, e.g. "AU= mg/L"

2. Determine what you already know.
     a. What are you given by the problem, if anything? Example: "In one minute, you counted 45 drops."
          • Rephrase if necessary. Think: "Drip rate is 45 drops per minute."
          • Translate into math terms using abbreviations, e.g. "45 gtt/min"
               — If a given is in the form mg/kg/day, rewrite as mg/kg x day (see example 8)
               — If a percentage is given, e.g. 25%, rewrite as 25/100 with appropriate labels (see example 4)
     b. Determine conversion factors that may be needed and write them in a form you can use, such as
         "60 min/1 hour." You will need enough to form a "bridge" to your answer unit(s). See example 1.
          • Factors known from memory: You may know that 1 kg = 2.2 lb, so write down "1 kg/2.2 lb"
               and/or "2.2 lb/1 kg" as conversion factors you may need.
          • Factors from a conversion table: If the table says "to convert from lb to kg multiply by 2.2," then
               write down "2.2 lb/1 kg"

3. Setup the problem using only what you need to know.
     a. Pick a starting factor.
          • If possible, pick from what you know a factor having one of the units that's also in your answer
               unit and that's in the right place. See example 1.
          • Or pick a factor that is given, such as what the physician ordered.
          • Note that the starting factor will always have at least one unit not in the desired answer unit(s) that
               will need to be changed by canceling it out.
     b. Pick from what you know a conversion factor that cancels out a unit in the starting factor that you
          don't want. See example 1.
     c. Keep picking from what you know factors that cancel out units you don't want until you end up with
          only the units (answer units) you do want.
     d. If you can't get to what you want, try picking a different starting factor, or checking for a needed
          conversion factor.
     e. If an intermediate result must be rounded to a whole number, such as drops/dose which can only be
          administered in whole drops, setup as a separate sub-problem, solve, then use the rounded off
          answer as a new starting factor. See example 10.

4. Solve: Make sure all the units other than the answer units cancel out, then do the math.
     a. Simplify the numbers by cancellation. If the same number is on the top and bottom, cancel them out.
     b. Multiply all the top numbers together, then divide into that number all the bottom numbers.
     c. Double check to make sure you didn't press a wrong calculator key by dividing the first top number
          by the first bottom number, alternating until finished, then comparing the answer to the first one.
          Miskeying is a significant source of error, so always double check.
     d. Round off the calculated answer.
          • Be realistic. If you round off 74.733333 to 74.73 mL that implies that all measurements were of
               an extreme accuracy and that the answer is known to fall between 74.725 and 74.735, or 74.73
               + 0.005 mL. A more realistic answer would probably be 74.7 mL or 75 mL. See example 6.
          • If you round to a whole number that implies a greater accuracy than is appropriate, write your
               answer to indicate a range, such as 75 + 5 mL. See example 10.
     e. Add labels (the answer unit) to the appropriately rounded number to get your answer. Compare
          units in answer to answer units recorded from first step.

5. Take a few seconds and ask yourself if the answer you came up with makes sense. If it doesn't,
     start over.

This is a fairly bare outline. The steps are best taught, rather than read, and so would serve better as a guide to tutoring students than as a self-teaching guide.

A copy of the above guide in Word format is available, click here. Also see Medication Math for the Nursing Student which contains this page and is also available as a Word document.

Support this site: Visit our Zazzle store featuring ultra hi-res images of artworks, Hubble/ESA/NASA space images, Mandelbrot fractals, maps and more. Images up to 525 megapixels allow for fine printing at the largest sizes. Give a fine print as a gift that could hang around for a hundred years.

One of many How-to videos on YouTube.

• Webmaster
• Privacy Policy
• Contact