1. How many seconds are in a day?

Not a med-math problem, but as an introduction to dimensional analysis (DA), it works fine. If you're up to speed in DA, skip this answer. Otherwise, what do you do? First, as with all DA problems, don't panic. If you have no idea what the answer is or how to come up with an answer, that's fine because you're not going to solve THE problem. What you are going to do is break the problem down into several small problems that you can solve, and here's how.

a. Ask yourself, "What units of measure do I want to know or have in the answer? " In this problem you want to know "seconds in a day." After you figure out what units you want to know, translate the English into Math. Math is a sort of shorthand language for writing about numbers of things. If you can rephrase what you want to know using the word "per," then that's a step in the right direction, so rephrase "seconds in a day" to "seconds per day." In math terms, what you want to know is:

b. Ask, " What do I know? " What do you know about how "seconds" or "days" relate to other units of time measure? You know that there are 60 seconds in a minute. You also know that in 1 minute there are 60 seconds. These are two ways of saying the same thing. You know that there are 24 hours in a day (and in one day there are 24 hours). If you could now connect "hours" and "minutes" together you would have a sort of bridge that would connect "seconds" to "days" (seconds to minutes to hours to days). The connection you need, of course, is that there are 60 minutes in an hour (and in one hour there are 60 minutes). When you have this kind of connection between units, then you know enough to solve the problem--but first translate what you know into math terms that you can use when solving the problem. If in doubt, write it out:

All of these statements, or conversion factors, are true or equivalent (60 seconds = 1 minute). All you need to do now is pick from these statements the ones that you actually need for this problem, so....

c. Ask, "From all the factors I know, what do I need to know ?"

Remember that you want to know:

So pick from the things you know a factor that has seconds on top or day(s) on the bottom. You could pick either of the following two factors as your "starting factor:"

Write down your starting factor (say you pick 60 seconds per 1 minute):

Now the trick is to pick from the other things you know another factor that will cancel out the unit you don't want. You start with "seconds" on top. You want "seconds" on top in your answer, so forget about the seconds--they're okay. The problem is you have "minutes" on the bottom but you want "days." You need to get rid of the minutes. You cancel minutes out by picking a factor that has minutes on top. With minutes on top and bottom, the minutes will cancel out. So you need to pick 60 minutes per 1 hour as the next factor because it has minutes on top:

You now have seconds per hour, since the minutes have cancelled out, but you want seconds per day, so you need to pick a factor that cancels out hours:

d. Solve it. When you have cancelled out the units you don't want and are left only with the units you do want, then you know it's time to multiply all the top numbers together, and divide by all the bottom numbers.

In this case you just need to multiple 60x60x24 to get the answer: There are 86,400 seconds in a day.

Here's how this problem might look if it were written on a chalkboard:

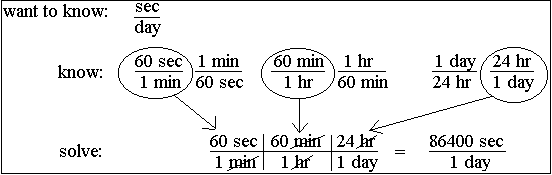
Remember that you don't need to worry about the actual numbers until the very end. Just focus on the units. Plug in conversion factors that cancel out the units you don't want until you end up with the units you do want. Only then do you need to worry about doing the arithmetic. If you set up the bridge so the units work out, then, unless you push the wrong button on your calculator, you WILL get the right answer every time.

2. You are to give "gr 5 FeSO₄" but the available bottle gives only the milligrams of iron sulfate per tablet (325 mg/tab). How many milligrams is the order for?

To get from grains to milligrams you'll need a conversion factor like 1 gr = 64.8 mg.

5 gr x 64.8 mg = 324 mg, so you decide that's close enough and give 1 tab.
             1 gr

Rounding to 60 mg/1 gr, as is often done, gives 300 mg as your answer, which might cause you to doubt if you will be giving the ordered dose.

3. You just opened a 500 mL bottle of guaifenesin and will be giving 1 tablespoon per dose. How many doses are in the bottle? In other words how many tablespoons are in 500 mL?

500 mL x 1 tsp   x 1 tbs = 33 tbs
               4.93 mL  3 tsp

Rounding to 5 mL gives you the same answer, so rounding to 5 mL is reasonable.

4. You give your home health patient an unopened 500 mL bottle of guaifenesin and tell them to take 2 teaspoons 4 times a day as ordered. They ask you how long the bottle will last.

You could give an answer in hours or weeks, but you figure "days" is the better choice for an answer unit. Your set up:

500 mL x 1 tsp x 1 dose x 1 day    = 12.5 days,
               5 mL     2 tsp      4 doses

 so you tell them the bottle will last 12 days.

5. Your order is for meperidine (Demerol) 35 mg, IM, STAT. Available is a 2 mL vial containing 50 mg/mL meperidine. On hand are 1 mL and 3 mL syringes. How much should you draw up into which syringe?

Your answer will be in mL (cc), the number of milliliters that will contain 35 mg meperidine. You know from the label that there is 50 mg meperidine in 1 mL of meperidine solution. You realize you will give less than 1 mL. Your set up:

35 mg mep. x 1 mL mep. sol = 0.7 mL mep. sol
                        50 mg mep.

or, since you know that you want "mL on top" in your answer, you could start with 1 mL/50 mg:

1 mL x 35 mg = 0.7 mL
50 mg

If you don't actually write down full labels, at least be thinking "mL of what?" "mg of what?"

6. You are shadowing a nurse during a clinical who receives an order to adjust the infusion rate of a pump so that 1.6 mg of lidocaine are being delivered per minute. Hanging is a 100 mL piggyback containing 0.4 grams lidocaine, a 0.4% solution. Without writing anything down, the nurse tries to solve the problem on a calculator. After the fifth different and incorrect answer you find a piece of scratch paper and offer to show her how to set up the problem. She assures you she can always do problems like this on tests, but admits that at the moment her brain doesn't seem to be working. How would you set up and explain the problem to her?

We want to know mL/hr, which has "time" on the bottom so starting with 1.6 mg/min should work. We now just have to change minutes to hours, and get from mg to mL.

1.6 mg L. x 60 min x 100 mL L. sol = 24.0 mL L. sol
   1 min         1 hr        400 mg L.                    hr

Checking to make sure all the units of measure, except for mL and hr, cancel out, now is the time for the calculator. Crunching the numbers twice (first x x x ¸ ¸ , then x x ¸ x ¸ ) and getting 24.0 each time, we can now set the pump with confidence.

7. On your first day of clinicals at a long-term care facility you are caring for a resident receiving total enteral feeding through a PEG tube. He is receiving 60 mL Jevity per hour as ordered when the pump fails and no other pumps are available. His over-extended regular nurse hangs drip tubing, adjusts the drip rate to something that "looks about right," and rushes on to her next demand. You decide to adjust the drip rate accurately to give the ordered amount. What do you need to know to do so?

You look in the trash for the tubing package, but don't see it. You recall seeing tubing in the supply room and go there looking for the same tubing as what was hung. The reason is drop size varies from 8 to 60 drops per mL. The manufacturer would have calibrated their drip chamber and put the number of drops/mL on the package, and it is the drop factor (drops/mL) that you need to know. You finally find the tubing used and the package says 12 drops/mL. Your answer will be in drops/min, so:

60 mL x 12 drops x 1 hr    = 12 drops
 1 hr         1 mL      60 min          min

or 3 drops every 15 seconds which is easier to count. It turns out that "about right" was about twice the ordered rate.

8. Your hospice patient is on a double pump. One side is running NS at 30 mL/hr KVO, and the other has a 100 mL bag containing 2 mg morphine sulfate (MS) running at 5 mL/hr for pain management. She begins to show signs of breakthrough pain and her doctor orders 0.2 mg MS STAT. You would normally use a prefilled syringe containing 1 mg/1 mL MS and give 0.2 mL IV push, but on looking in the narcotic cabinet you find none available and the pharmacy is closed. It occurs to you that you could reset the pump to deliver 0.2 mg MS in 5 minutes, then go back to 5 mL/hr. At what rate should you set the pump?

Again you want mL/hr, so start with mL on top:

100 mL MS sol x 0.2 mg MS x 60 min = 120 mL MS sol
   2.0 mg MS          5 min              1 hr                hr

Now that you know the rate, you need the volume to be infused:

100 mL MS sol x 0.2 mg MS = 10 mL MS sol
   2.0 mg MS

Just to double check, how many minutes will it take for the pump to deliver 10 mL at 120 mL/hr?

60 min x  1 hr     x  10 mL = 5 min
 1 hr        120 mL

9. A textbook on clinical calculations includes the following conversion for household to metric: 1 teaspoon = 5 mL = 5 g. As a home health nurse you need to help a client make homemade pediatric electrolyte solution using the following recipe: 1 L boiled water, 30 g sugar, 1.5 g salt, 2.5 g lite salt (KCl), 2.5 g baking soda. Since only kitchen measuring cups and spoons are available you need to convert from metric. The answer, according to the textbook, is 1 qt boiled water, 2 tbsp sugar, 1/4 tsp salt, 1/2 tsp lite salt, and 1/2 tsp baking soda. What questionable assumption does the textbook make?

While 1 tsp = 5 mL is a valid conversion factor, 1 tsp = 5 g is valid only when measuring water. "Teaspoon" is a measure of fluid volume and not weight. Since water has a density of 1 (1 g/1 mL), 1 tsp of water would weigh 5 grams. The density of salt, however, is 2.2 g/mL (sugar 1.6, KCl 2.0, NaHCO₃ 2.2), so a teaspoon would weight over twice as much, right? But wait, these densities are for the solid substances. In powdered form they would weigh less. A teaspoon of salt (density 1.3 g/mL) would weigh 6.5 grams. The density of granulated sugar is 0.7 g/mL, KCl is 1.0 g/mL, and baking soda is 0.8 g/mL, so a teaspoon of each would actually weigh between 3.5 g/mL and 6.5 g/mL. Assuming 5 g/tsp for each seems a bit rough. To do the conversions right, factor in the density:

Sugar: 30 g x 1 mL x 1 mL x 1 tsp x 1 tbsp = 2.9 tbsp (not 2.0 tbsp)
                      0.7 g    1 mL    5 mL    3 tsp

Salt: 1.25 g x 1 mL x 1 tsp = 0.2 tsp (close to 1/4 tsp)
                         1.3 g    5 mL

Baking soda: 2.5 g x 1 mL x 1 tsp = 0.63 tsp (closer to 2/3 than 1/2)
                                      0.8 g    5 mL

KCl, with density 1, remains at 1/2 tsp. Does taking the density into account really matter? Realizing that density is something to take into account matters, and until you look up the densities and factor them in you wouldn't know if it matters or not.

10. In another textbook you are given the following example: Order: Chloromycetin 300 mg 1V bolus via saline lock. Label: Chloromycetin 1 g. Directions: Reconstitute with 10 mL sterile water for injection to yield 100 mg/mL. How may mL of Chloromycetin should be administered?

Equivalents: 1 g = 10 mL, 1000 mg = 1 g

300 mg x 1 g      x 10 mL  = 3 mL
              1000 mg   1 g

While the answer "3" happens to be right, the set up is not. What error did the textbook make?

The set up is in error due to a failure to fully label units. The 10 mL is "10 mL sterile water." You have to ask, "10 mL of what?" Your answer unit, what you want to know, is "mL Chloromycetin sol" and not just "mL." You can't use "mL water" and end up with "mL Chlor. sol." When you add 10 mL water to reconstitute you will end up with somewhat more than 10 mL Chlor. solution. Since you want "mL Chlor. sol" in your answer, pick a factor that has "mL Chlor. sol" in it and in the right place. You are given "100 mg/mL" which should be more completely written as "100 mg Chlor./mL Chlor. sol" and "10 mL/g" should be "10 mL water/1 g Chlor." which is quite an unnecessary bit of information for solving this problem, though the text incorrectly uses it.

300 mg Chlor. x 1 g Chlor.    x   10 mL water = 3 mL water (not!)
                          1000 mg Chlor.    1 g Chlor.

The correct set up should be:

300 mg Chlor. x 1 mL Chlor. sol = 3 mL Chlor. sol
                              100 mg Chlor.

11. How would you prepare 2 L of 3% sodium hypochlorite (bleach) and water solution? You have only a measuring cup.

2 L sol x 1000 mL x 3 mL bleach x 1 oz   x 1 cup = 1/4 cup bleach
                   1 L         100 mL sol    30 mL  8 oz

But how much water? The solution is 97% water, right?

2 L sol x 1000 mL x 97 mL water x 1 oz    x 1 cup = 8.1 cups water
                     1L         100 mL sol    30 mL    8 oz

12. In a home setting, how would you prepare 1 L (or so) of normal saline (0.9% NaCl) using water and table salt if you have only a measuring cup and a teaspoon? On hand is an unopened 1 lb box of salt.

The key is to clearly understand what 0.9% means. Salt is measured by weight, so 0.9% means 0.9 parts salt by weight to 100 parts salt solution (not water) by weight. If you knew the density of granulated salt you could convert from a desired weight of salt to a volume of salt. Since you can only measure volume (using cup and tsp), you will somehow have to determine the density of salt. You could look up the density, or what if you poured the box of salt (16 oz) into your measuring cup? Doing so you find that you have a bit over 12 fluid ounces of salt. Recalling that density is weight/volume, you figure the density of salt at 16 oz/12.3 fl oz or 1.3 oz/fl oz. What you want to know is the number of teaspoons per quart. The set up follows:

12.3 fl oz salt x 0.9 oz salt       x 32 oz  x 2 tbsp  x 3 tsp = 1 1/3 tsp salt
16 oz salt         100 oz salt sol    1 qt        1 fl oz    1 tbsp           qt salt sol

To make one quart you would first put the salt into a measuring cup then fill to the 1 quart mark.

13. You have an order to infuse 1000 mL of D5W (5% Dextrose in water) IV over a period of 5 hr. No pump is available, but the tubing set package notes that the drop factor is 10 gtt/mL. How would you adjust the drip rate?

First, what do you want to know? The flow rate in gtt/min, which are the answer units. What do you know? You're given that there are 10 gtt/mL and that the infusion rate is 1000 mL/5 hr. Since you want gtt on top and 10 gtt/mL has gtt in the right place, 10 gtt/mL makes a perfectly good starting factor--from there you just need to get from mL to min. The set up then:

10 gtt x 1000 mL x 1 hr    = 33 gtt
 1 mL      5 hr        60 min         min

You wouldn't want to count a full minute, so divide by 3 and count for 20 seconds.

14. The order is for meperidine 60 mg and atropine gr 1/150, IM. The meperidine on hand is 100 mg/mL and the atropine is 0.4 mg/mL. The two are compatible so you plan to draw up both in the same syringe. How much of each will you draw up?

For both you want to know mL, your answer unit.

60 mg x 1 mL   = 0.6 mL meperidine
            100 mg

1 gr x 64.8 mg x 1 mL    = 1.1 mL atropine
150       1 gr       0.4 mg

15. Tagamet is ordered 200 mg, IV, q6h. Available is Tagamet 300 mg in a 2 mL vial of aqueous solution. You are to dilute a portion of this in 100 mL NS and infuse over 20 minutes using a Buretrol with a drop factor of 60 gtt/mL. How much Tagamet will you inject into the Buretrol, and what will the drip rate be?

You want to know mg of Tagamet, and gtt/min.

200 mg T.   x 2 mL T. sol = 1.3 mL T.
100 mL NS    300 mg T.      100 mL NS

The drip rate would be:

60 gtt x 101.3 mL T. sol = 304 gtt T. sol
1 mL         20 min                         min

Can you count 5 gtt/sec? Not likely, so what do you do? What if you added a secondary set with a drop factor of 12 gtt/mL?

12 gtt x 101.3 mL T. sol = 60 gtt T. sol
1 mL        20 min                       min

16. The order is for amoxicillin 60 mg, po, tid for a child weighing 13 lb. The pediatric dosage range is 20-40 mg/kg/day in three equal doses. Is the dose safe?

You want to know mg/kg/day for this child. What you know is that you will give 60 mg per 13 lb body weight per dose or 60 mg/13 lb/dose, which true but is unusable in this form, so you rewrite it as 60 mg/13 lb x 1 dose. How can you do that? Consider dividing 1/4 by 2. Half of one quarter is one eighth, but how to figure that:

1 = 1 x 1 =    1    =   1
4    4    2    4 x 2       8
2

Dividing by 2 is the same as inverting 2 to get 1/2 and multiplying. Acceleration, to give another example, is measured in feet per second per second or ft/sec/sec, which is equal to ft/(sec x sec) or ft/sec².

 

60 mg             x 2.2 lb x 3 dose = 30.5 mg        = 30.5 mg/kg/day--a safe dose.
13 lb x 1 dose   1 kg      1 day              kg x day

Whenever you have x per y per z, rearrange in the form x/y*z and everything will stay straight.

17. A child with severe poison ivy weighs 25 kg and Benadryl po 5 mg/kg/day is ordered q6h. Benadryl is available as a 12.5 mg/5 mL solution. What dose should be given?

You want to know mL/dose. Since you want mL on top, start with:

5 mL     x 5 mg      x 1 day     x 25 kg = 12.5 mL
12.5 mg   kg x day    4 doses                        dose

18. You are to infuse heparin 25000 U in 250 mL NS at 10.6 mL/hr. What is the concentration of heparin solution? When you clear the pump you note that 67 mL have been infused. How much heparin has been given?

You want to know Units/mL, so nothing tricky here:

25000 U = 100 U/mL
 250 mL

67 mL sol x 100 U    = 6700 U
                   mL sol

19. Your patient weighs 143 lb, and you are ordered to infuse 250 mg dobutamine in 500 mL NS at 10 mcg/kg/min. How many milligrams of dobutamine will infuse per hour?

You want to know mg/hr, which has time on the bottom. After converting to 10 mcg/kg x min you note that time is also on the bottom, so this should work as a starting factor:

10 mcg  x 60 min  x  1 mg       x  1 kg     x 143 lb = 39 mg
kg x min     1 hr       1000 mcg    2.2 lb                          hr

20. Phenobarbital 180 mg/m²/24 hours given every eight hours is ordered for a child whose BSA (body surface area) is 0.29 m². How much will each dose be?

You want to know mg/dose, so you could start with 1 day/3 doses or 180 mg/m²/day:

1 day   x 180 mg   x 0.29 m² = 17.4 mg
3 doses   m² x day                            dose

21. You are to give Lidocaine 30 mcg/kg/min to a child weighing 55 lb. The piggyback contains 120 mg Lidocaine in 100 mL NS. At what rate will you set the pump?

You want to know mL/hr. Starting with the patient's weight usually works out:

55 lb x 1 kg    x 30 mcg   x  1 mg       x 100 mL x 60 min = 37.5 mL
            2.2 lb    kg x min    1000 mcg   120 mg       1 hr                hr

22. Nipride is ordered and you are to titrate to maintain the systolic blood pressure at 150 mm Hg. Available is Nipride 50 mg/250 mL. The range is 3-6 mcg/kg/min. A microdrip chamber (60 gtt/mL) is used with a pump. Your patient weighs 135 lb.

Titration problems are just longer, not more difficult, so relax and focus on what you want to know.

What is the concentration of the solution in mcg/mL?

Here you want mcg/mL, so:

50 mg   x 1000 mcg = 200 mcg/mL
250 mL     1 mg

How many mcg/min, lower and upper range, could be administered?

3 mcg    x 1 kg x 135 lb = 184 mcg low range
kg x min   2.2 lb                         min

Since the high range is twice the low, just multiple by 2 to get 368 mcg/min.

Within what range will the pump rate be set?

What's the low and high rate the pump could be set at in mL/hr?

184 mcg x 60 min x 1 mL      = 55 mL low range,
  1 min        1 hr      200 mcg            hr

which is also 55 gtt/min: 55 mL x 1 hr     x 60 gtt = 55 gtt
                                               1 hr       60 min   1 mL          min

You could plug in 368 for 184 and recalculate, or again just double 55 to get 110 mL/hr for the upper range.

What is the titration factor in mcg/gtt for the low range?

Don't know what a titration factor is? It don't matter 'cause you know you want mcg/gtt:

184 mcg x 1 min = 3.3 mcg
  1 min      55 gtt           gtt

The patient's systolic BP is currently 170 mm Hg while receiving the low range dose. If you increase the gtt/min by 5 gtt, how many mcg/min will the patient be receiving?

You want mcg/min and from the above, going from 55 to 60 gtt/min:

3.3 mcg x 60 gtt = 198 mcg
1 gtt         1 min              min

After 1 hr, the systolic blood pressure is 120 mm Hg, so you decrease the gtt/min by 6 gtt. How many mcg/min is the patient now receiving?

You again want mcg/min and are going from 60 to 54 gtt/min:

3.3 mcg x 54 gtt = 178 mcg
  1 gtt       1 min            min

23. How would you prepare 500 mL of a 1:35 bleach solution from a 1:10 bleach solution using water?

You want to know how much concentrated bleach solution (mL c.b.) you need to make the weaker solution (mL w.b.).

10 mL c.b. x 1 mL b.      x 500 mL w.b. = 143 mL c.b.
  1 mL b.      35 mL w. b.

To the 143 mL of concentrated bleach solution you would add enough water to make 500 mL 1:35 solution. If you fully label all amounts, you should avoid confusion.

24. Dr. Kissoff, wishing to test your perspicacity, orders 1.9 milliscruples of Morphine IV for each stone of body weight to be administered over a 300-minute period. Available is 1 gill of Morphine (MS) solution having a concentration of 0.4 pennyweights of Morphine dissolved in 1000 drachms of solution. The patient weighs 79 kilograms. At what rate should you set the pump? Your drug guide says that 0.8 to 10 mg of morphine can be given per hour. Is the ordered dose safe? (Yes, all the units of measure are real, if seldom used, but the point is you don't even have to know what the units are, just how to get from what you are given to what you want to know. See the long list of Conversion factors for clues, then use the Back button on your browser to return.)

Breaking the problem down stepwise: As always, start by asking what do you want to know? If you've worked with IV pumps you know they are programmed in mL/hr, so your answer will have to be in these units of measure.

What do you know? From the problem you know the patient weighs 79 kg, and that you are to infuse 0.0019 scruples per stone per 300 minutes (it helps to rephrase the problem using the word "per"). You are also told that there are 0.4 pennyweights MS per 1000 drachms and that you have a whole gill of this solution however much a gill is. You also know that since you need "hours" in your answer you will need to get from minutes (300 minutes) to hours at some point. And everyone knows that in 1 hour there are 60 minutes and in 60 min. there is 1 hr. (or in math terms you know 60 min/1 hr, and 1 hr/60 min).

The rest of what you need to know will have to be looked up. Doing so you find that there are 4 ounces per gill, 20 grains per scruple, 24 grains per pennyweight, and 3.55 milliliters per drachm. Looking up "stone" you find that there are 0.14 centals per stone, which forces you to lookup "cental" where you find that there are 45.36 kilograms per cental.

3. Setup: What factor should you start with? Since you know that the patient's weight is a determining factor, you could start with it. Or, since you know your answer has to be in mL/hr, you know "hours" has to be on the bottom, so 60 min/1 hr would be a logical starting factor (you would then just have to get from "min" to "mL"). Or, since you want "mL" on top, 3.55 mL/drachm would also be a logical starting factor. If you recall the Commutative Law of Multiplication, you realize you get the same answer no matter what order you multiply (or divide) your terms in, but you decide to pick 79 kg as your starting factor.

  79 kg x 1 cental x 1 stone    x     0.0019 scruples   x 60 min x 20 grains x 1 pennyweight x 1000 drachms x 3.55 mL = ? mL
              45.36 kg   0.14 centals   1 stone x 300 min     1 hr       1 scruple         24 grains          0.4 pennywts   1 drachm     hr

Does everything cancel out except for "hr" and "mL"? Bingo, punch the numbers in (correctly) and you got it: 35 mL/hr. Does the answer make sense? The flow rate is within usual limits, but is the dose safe? Go back to step 1: you'll need to know mg/hr, your answer unit, and you'll need a conversion factor to get from grains to milligrams. Since you need "hr" on the bottom, start with 35 mL/hr.

35 mL x 1 drachm x 0.4 pennyweights x   24 grains       x   64.8 mg = 6.1 mg
 1 hr        3.55 mL       1000 drachms       1 pennyweight     1 grain            hr

The dose is safe, but on the high side, so you'll be monitoring your patient closely. Oh, and since you have 1 gill (4 ounces) or about 120 mL of morphine solution, are you going to have enough? Go figure.

25. You have come down with a bad case of the geebies, but fortunately your grandmother has a sure cure. She gives you an eyedropper bottle labeled:

Take 1 drop per 15 lb of body weight per dose four times a day until the geebies are gone. Contains gr 8 heebie bark per dr 100 solvent. 60 drops=1 tsp.

You weigh 128 lb, and the 4-oz bottle is half-full. You test the eyedropper and find there are actually 64 drops in a teaspoon. You are going on a three-week trip and are deeply concerned that you might run out of granny's geebie tonic. Do you need to see her before leaving to get a refill?

Now this one is a bit hard if you haven't been paying close attention.

First, what do you want to know? You want to know how long the bottle will last. You could figure out days/bottle or weeks/bottle and see if the bottle will last longer than 3 weeks or 21 days. So you write down "Answer units = days/bottle"

What do you know to start off with that you might need to know? You write down the following:

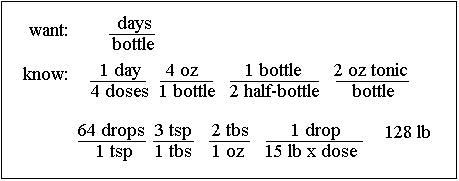
You realize that if a 4-oz bottle is half-full, then there is 2 oz of tonic in it, but you could figure it out dimensionally if you wanted to:

You would then end up with "days/half-bottle" in your answer, but it's easier to just go with 2 oz/bottle.

What should you use as a starting factor? You pick 128 lb because it's something you're given and starting with weight usually works. You set the problem up:

Houston, we have a problem. You ended up with units reversed from what you wanted. You figured out how much of the bottle you would use in one day. What to do? You could hit the 1/x button on your calculator if it had one, or invert the answer by dividing 1 by 0.044, or start over with 128 lb on the bottom. What? Can you do that? Sure you can. You could even put 128 lb on the end and on the bottom, or put it in the middle somewhere. You decide to start over, this time picking a starting factor that already has "day" or "bottle" in the right place.

So, it looks like you'll have enough. At some point you need to know how many drops per dose you will need to take, so you figure it out:

As a practical matter, you can't take 8.533 drops per dose; you have to round off. At this point you realize that when you calculated 22.5 days/bottle, you were not figuring on 9 drops/dose. You decide to recalculate to see if rounding up to 9 makes a significant difference.

You note a small difference, but conclude that you have just enough geebie tonic. Concluding that you have enough, however, and having enough may not be the same thing. The story continues:

You leave on your trip and on the 19th day you run out of geebie juice. You didn't spill any, and no one took any. You sit in a stunned stupor trying to figure out where you went wrong in your calculations.

You finally realize there might not have been 2.0 oz of tonic in the bottle to begin with. A measurement like "half a bottle" should not inspire great certainty. You wish you had measured the amount and found that the bottle contained 2.0 + 0.05 oz of tonic, but what you were given, more or less, was that you had 2 + 0.5 oz of tonic. There could be anything from 1.5 to 2.5 oz in the bottle. Recalculating using the low and high values, you find you had enough tonic to last somewhere between 16 and 26 days. If you had figured out the correct answer of 21 + 5 days the first time, you would have realized you had only slightly less than a 50/50 chance of running out, and would have gone to see Granny for a refill.

Support this site: Visit our Zazzle store featuring ultra hi-res images of artworks, Hubble/ESA/NASA space images, Mandelbrot fractals, maps and more. Images up to 525 megapixels allow for fine printing at the largest sizes. Give a fine print as a gift that could hang around for a hundred years.

One of many How-to videos on YouTube.

• Webmaster
• Privacy Policy
• Contact